Приращение функции $\Delta $y равно величине отрезка BD (рис.1). Дифференциал dy равен величине отрезка ВС, где С -- точка пересечения касательной Т с вертикальной прямой, проходящей через точку х + $\Delta $х оси Ох.
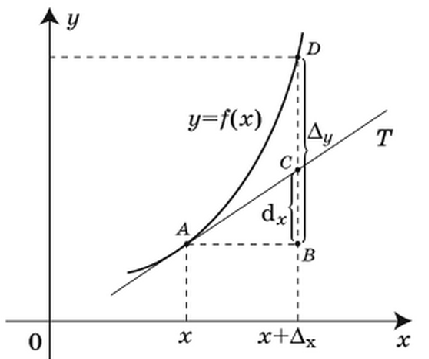
Рисунок 1. Геометрический смысл дифференциала
Таким образом, геометрический смысл дифференцирования заключается в приращении ординаты касательной, соответствующей приращению аргумента dx = $\Delta $х. Значит, dy = y`dx, а дифференциал функции равен произведению ее производной на приращение независимой переменной.
Определить приращение и дифференциал функции y = 2х3+5 при переходе х от значения 1 к значению 1,05.
Решение.
- Определим приращение заданной функции при произвольных значениях х и $\Delta $х. \[dy=y'dx=6x^{2} dx\] \[\Delta y=2(x+\Delta x)^{3} +5-2x^{3} -5=2x^{3} +6x^{2} \Delta x+6x\Delta x^{2} +2\left(\Delta x\right)^{2} +5-2x^{3} -5\] \[\Delta y=6x^{2} \Delta x+6x\Delta x^{2} +2\left(\Delta x\right)^{2} \]
- Найдем приращение аргумента. \[\Delta x=1,05-1=0,05\]
- Подставим числовые значения в равенство приращения функции \[\Delta y=6\cdot 1^{2} \cdot 0,05+6\cdot 1\cdot 0,05^{2} +2\left(0,05\right)^{2} =0,3+0,015+0,005=0,32\]
Доказать, что если $\Delta $х -- бесконечно малая величина, то с точностью до бесконечно малой высшего порядка имеет место приближенное равенство sin $\Delta $х ≈ $\Delta $х
Доказательство.
Рассмотрим функцию y = sinx. Приращение этой функции $\Delta $y = sin (x + $\Delta $х) -- sinx, а ее дифференциал dy = cosx $\Delta $х. Поскольку $\Delta y\approx dy$:
sin (x + $\Delta $х) -- sinx ≈ cosx $\Delta $х
sin (x + $\Delta $х) ≈ cosx $\Delta $х + sinx
Предположим что $х = 0$, тогда формула имеет вид:
sin (0 + $\Delta $х) ≈ cos0 $\Delta $х + sin0
sin $\Delta $х ≈ $\Delta $х
Формула, полученная в доказательстве примера 2, показывает, что для малых углов (в радианах) синус равен числу радиан, содержащихся в угле.
sin $\Delta $х ≈ $\Delta $х
Например, 40 = 0,0698, значит sin0,0698 ≈ 0,0698.
Прямым измерением найдено, что диаметр круга равен 5,2 см, причем максимальная погрешность измерения составляет 0,01. Найти приближенную относительную и процентную погрешности в вычисленной площади этого круга.
Решение.
Относительная погрешность вычисления площади находится по формуле:
\[\delta _{s} =\frac{\Delta s}{s} \]Приближенное значение получается в следствие замены $\Delta $s на ds. Поэтому приближенный расчет будет производиться по формуле:
\[\delta _{s} =\frac{ds}{s} \]Поскольку площадь круга с радиусом х равна:
\[s=\frac{1}{4} \pi x^{2} \] \[ds=\frac{1}{2} \pi xdx\]Таким образом,
\[\delta _{s} =\frac{\frac{1}{2} \pi xdx}{\frac{1}{4} \pi x^{2} } =2\frac{dx}{x} \]Заменим х и dx числовыми значениями
\[\delta _{s} =2\frac{0,01}{5,2} \approx 0,004\](что составляет погрешность 4%)
Доказать, что приближенная относительная погрешность вычисленного объема шара равна утроенной погрешности в измерении его диаметра.
Решение.
Объем шара с диаметром х вычисляется по формуле:
\[V=\frac{1}{6} \pi x^{3} \]Погрешность вычислений $\Delta $V приближенно равна
\[dV=\frac{1}{2} \pi x^{2} dx\]Тогда относительная погрешность составит:
\[\delta _{V} \approx \frac{dV}{V} \] \[\delta _{V} \approx \frac{\frac{1}{2} \pi x^{2} dx}{\frac{1}{6} \pi x^{3} } \] \[\delta _{V} \approx 3\frac{dx}{x} \]Поскольку относительная погрешность измерения диаметра равна:
\[\delta _{x} \approx \frac{dx}{x} \]То относительная погрешность равна:
\[\delta _{V} \approx 3\delta _{x} \]











