Пусть $y = f(x)$ и $x = \varphi (y)$ -- взаимно обратные функции. Тогда если функция $y = f(x)$ имеет не равную нулю производную $f'(x)$, то обратная функция имеет производную $\varphi '(y)$.
$\phi '(y)=\frac{1}{f'(y)} $ или $x'_{y} =\frac{1}{y'_{x} } $
Поскольку $y = f(x)$ и $x = $ $\varphi (y)$ -- взаимно обратные функции, то x = $\varphi (f(x))$. Применяя дифференцирование, получаем:
Найдем производную функции y=arcsinx, воспользовавшись правилом дифференцирования обратной функции. Обратной данной является функция $x = siny$.
Поскольку $\arcsin x=\sqrt{1-x^{2} } $. Таким образом,
Аналогично выводится равенство для:
Полученные формулы справедливы для отрезка $-1
Найдем производную функции $y = arctgx$. Обратной к ней будет функция $x = tgy$.
Условия дифференцируемости выполнены. Значит:
Аналогично выводится равенство для:
Найти производную функции
\[y=\arcsin x\cdot \arccos x\]Решение.
- Воспользуемся дифференцированием: \[y'=\left(\arcsin x\cdot \arccos x\right){{'} } =arcsin'x\cdot \arccos x+\arcsin x\cdot arccos'x\] \[y'=\frac{1}{\sqrt{1-x^{2} } } \cdot \arccos x-\arcsin x\cdot \frac{1}{\sqrt{1-x^{2} } } \]
- Упростим выражение \[y'=\frac{\arccos x-\arcsin x}{\sqrt{1-x^{2} } } \]
Найти дифференциал в точке х = 1 при $\Delta $х = 0,08 функции
\[y=arctg^{3} \sqrt{x} \]Решение.
- Применим правило замены переменных: \[t=\sqrt{x} \] \[u=arctg\sqrt{t} \] \[y=u^{3} \]
- Воспользуемся дифференцированием: \[y'_{x} =y'_{u} \cdot u'_{t} \cdot t'_{x} =3u^{2} \cdot \frac{1}{1+t^{2} } \cdot \frac{1}{2\sqrt{x} } \] \[y'_{x} =3arctg^{2} \sqrt{x} \cdot \frac{1}{1+\left(\sqrt{x} \right)^{2} } \cdot \frac{1}{2\sqrt{x} } \]
- Упростим выражение \[y'_{x} =\frac{3arctg^{2} \sqrt{x} }{2\sqrt{x} \left(1+x\right)} \]
- Выполним замену $х = 1$ \[y'_{x=1} =\frac{3arctg^{2} \sqrt{1} }{2\sqrt{1} \left(1+1\right)} =\frac{3arctg^{2} 1}{4} =\frac{3}{4} \cdot \left(\frac{\pi }{4} \right)^{2} =\frac{3\pi ^{2} }{64} \]
- Тогда \[dy=y'dx=\frac{3\pi ^{2} }{64} \cdot 0,08=\frac{3\pi ^{2} }{800} \]
Найти производную функции
\[y=\arcsin (\sin x)\]Решение.
- Запишем производную \[y'=\frac{1}{\sqrt{1-\sin ^{2} x} } \cos x=\frac{\cos x}{\sqrt{\cos ^{2} x} } =\frac{\cos x}{\left|\cos x\right|} \]
- Можно сделать вывод, что если соsx принимает положительные значения -- производная равна единице, иначе не существует.
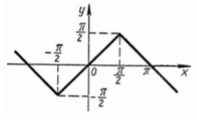График функции ">
Рисунок 1. График функции $y=\arcsin (\sin x)$
Найти производную функции
\[y=\arcsin e^{x} \]Решение.
\[y'=\left(\arcsin e^{x} \right){{'} } =\frac{1}{\sqrt{1-\left(e^{x} \right)^{2} } } \left(e^{x} \right){{'} } \] \[y'=\frac{1}{\sqrt{1-\left(e^{x} \right)^{2} } } \left(e^{x} \right){{'} } =\frac{e^{x} }{\sqrt{1-e^{2x} } } \]Найти производную функции
\[y=\left(\arcsin \frac{1}{x} \right)^{2} \]Решение.
\[y'=\left(\arcsin \frac{1}{x} \right)^{2} {{'} } =2\arcsin \frac{1}{x} \frac{1}{\sqrt{1-\frac{1}{x^{2} } } } \left(\frac{1}{x} \right){{'} } =-2\arcsin \frac{1}{x} \frac{1}{x\sqrt{x^{2} -1} } \]
