Одними из основных аспектов применения производной к исследованию функции являются: исследование функции на возрастание и убывание, исследование функций на выпуклость и вогнутость, нахождение точек экстремума функции, а также наибольшего и наименьшего значения функции. Рассмотрим их отдельно.
Экстремумы функции
Точки $x_0$ называются точками экстремума функции, если они являются точками максимума и минимума для функции $f(x)$.
$x_0$ называется критической точкой функции $f(x)$, если:
1) $x_0$ - внутренняя точка области определения;
2) $f'(x_0)=0$ или не существует.
Для исследования функции на существование точек экстремума, мы будем использовать теорему о достаточных условиях существования экстремума:
Достаточное условие экстремума
Пусть точка $x_0$ является критической для функции $y=f(x)$ и лежит в интервале $(a,b)$. Пусть на каждом интервале $\left(a,x_0\right)\ и\ (x_0,b)$ производная $f'(x)$ существует и сохраняет постоянный знак. Тогда:
1) Если на интервале $(a,x_0)$ производная $f'\left(x\right)>0$, а на интервале $(x_0,b)$ производная $f'\left(x\right)
2) Если на интервале $(a,x_0)$ производная $f'\left(x\right)0$, то точка $x_0$ - точка минимума для данной функции.
3) Если и на интервале $(a,x_0)$, и на интервале $(x_0,b)$ производная $f'\left(x\right)>0$ или производная $f'\left(x\right)
Схема исследования функции на экстремум
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f'\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать выводы о наличии максимумов и минимумов на каждом промежутке, используя теорему 2.
Монотонность функции
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Функция $y=f(x)$, определенная на промежутке $X$, называется возрастающей, если для любых точек $x_1,x_2\in X$ при $x_1f(x_2)$.
Функция $y=f(x)$, определенная на промежутке $X$, называется неубывающей, если для любых точек $x_1,x_2\in X$ при $x_1
Функция $y=f(x)$, определенная на промежутке $X$, называется невозрастающей, если для любых точек $x_1,x_2\in X$ при $x_1
Схема исследования функции на возрастание и убывание
1) Найти область определения функции $f(x)$;
2) Найти производную $f'(x)$;
3) Найти точки, в которых выполняется равенство $f'\left(x\right)=0$;
4) Найти точки, в которых $f'(x)$ не существует;
5) Отметить на координатной прямой все найденные точки и область определения данной функции;
6) Определить знак производной $f'(x)$ на каждом получившемся промежутке;
7) Сделать вывод: на промежутках, где $f'\left(x\right)0$ функция возрастает.
Наибольшее и наименьшее значение функции
Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наибольшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство
\[f\left(x\right)\le f(x_0)\]Функция $y=f(x)$, определенная на промежутке $X$, достигает своего наименьшего значения, если существует точка $x_0\in X$, такая, что для всех $x\in X$ выполняется неравенство
\[f\left(x\right)\ge f(x_0)\]Схема нахождения наибольшего и наименьшего значений функции $f(x)$ на отрезке $[a,b]$
1) Найти производную $f'(x)$;
2) Найти точки, в которых производная $f'\left(x\right)=0$;
3) Найти точки, в которых производная $f'(x)$ не существует;
4) Выбрать из полученных в пунктах 2 и 3 точек те, которые принадлежат отрезку $[a,b]$;
5) Вычислить значение функции в точках, полученных в пункте 4, а также на концах отрезка $[a,b]$;
6) Выбрать из полученных значений наибольшее и наименьшее значение.
Выпуклость и вогнутость функции
Функция $y=f(x)$, определенная на промежутке $X$, называется выпуклой, если для любых точек $x_1,x_2\in X$ выполняется неравенство
\[f\left(\frac{x_1+x_2}{2}\right)\le \frac{{f(x}_1)+f(x_2)}{2}\]Функция $y=f(x)$, определенная на промежутке $X$, называется вогнутой, если для любых точек $x_1,x_2\in X$ выполняется неравенство
\[f\left(\frac{x_1+x_2}{2}\right)\ge \frac{{f(x}_1)+f(x_2)}{2}\]Если в определении выпуклости и вогнутости функции нестрогие знаки заменить на строгие, то мы получим, соответственно, определение строго выпуклой и строго вогнутой функции.
Схема исследования функции на возрастание и убывание
1) Найти область определения функции $f(x)$;
2) Найти вторую производную $f''(x)$;
3) Найти точки, в которых выполняется равенство $f''\left(x\right)=0$;
4) Найти точки, в которых $f''(x)$ не существует;
5) Определить знак производной $f''(x)$ на каждом получившемся промежутке;
6) Сделать вывод: на промежутках, где $f''\left(x\right)0$ функция вогнута.
Задачи на применение производной
Исследовать функцию на возрастание, убывание, выпуклость, вогнутость и наличие точек максимумов и минимумов:$f(x)=\frac{x^2-2x+1}{4}$
Решение:
1) Область определения - все действительные числа;
2) $f'\left(x\right)=\frac{2x-2}{4}=\frac{x-1}{2}$;
3) $f'\left(x\right)=0$;
\[\frac{x-1}{2}=0\] \[x=1\]4) $f'(x)$ существует во всех точках области определения;
5) Координатная прямая:
Рисунок 1.
6) Определить знак производной $f'(x)$ на каждом промежутке:
\[f'\left(x\right) >0,\ при\ (1,+\infty )\] \[f'\left(x\right)7) Изобразим все на одном рисунке: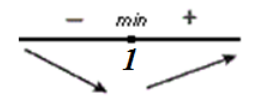
Рисунок 2.
Получаем:
Функция убывает, при $\left(-\infty ,1\right)$, функция возрастает, при $(1,+\infty )$.
Точка $x=1$ - точка минимума, точки максимума нет.
8) $f''\left(x\right)=\frac{1}{2}>0$
Функция вогнута на всей области определения.












