Особое значение в исследовании функций имеет применение нахождения максимумов и минимумов заданной функции при решении различных задач оптимизации. Данные задачи могут быть взяты из области алгебры, геометрии, физики.
При решении таких задач в общем случае используются знания теоремы Ферма.
Если заданная дифференцируемая функция $y=f(x)$ в точке $x=x_{0} $ имеет локальный минимум или максимум, то производная $f'(x)$ данной функции равна нулю в точке $x=x_{0} $.
С геометрической точки зрения теорему можно перефразировать следующим образом: касательная, проведенная к графику заданной функции $y=f(x)$ в точке $x=x_{0} $, параллельна оси абсцисс.
Алгоритм решения задачи на максимум/минимум:
- составление функции, описывающей зависимость из условия задачи;
- нахождение производной заданной функции;
- нахождение критических и стационарных точек;
- исследование знака $f'(x)$ с помощью числовой прямой;
- определение характера поведения функции;
- нахождение искомого максимума/минимума.
Алгебра
Разность двух положительных чисел равна 15, причем одно из чисел не больше 10. Найти такие числа, для которых произведение будет максимальным.
Решение:
Обозначения: $x$ - первое число, $y$ - второе число.
По условию задачи, $x-y=15$. Тогда $x=15+y$.
Запишем произведение чисел: $p(y)=y\cdot (15+y)=15y+y^{2} $.
Получаем исходную функцию: $p(y)=15y+y^{2} $.
Производная заданной функции: $p'(y)=(15y+y^{2} )'=15+2y$.
\[p(y)=0\Rightarrow 15+2y=0\Rightarrow y=-\frac{15}{2} =-7,5\]Исследуем знак $p'(x)$ с помощью числовой прямой (положительная полуось):
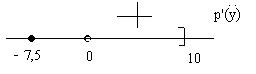
Рисунок 1.
Определим характер поведения функции
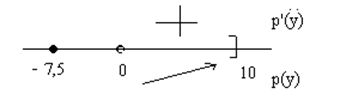
Рисунок 2.
Функция достигает максимума в точке $y=10$ (удовлетворяет условию задачи).
Вычислим второе число: $x=15+10=25$.
Следовательно, 10 и 25 -- искомые числа.
Геометрия
Какого размера должен быть цилиндр заданного объема $v=25$ (куб.ед.), чтобы его площадь полной поверхности была минимальной?
Решение:
Сделаем рисунок к задаче:
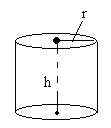
Рисунок 3.
Обозначения: $r$ - радиус основания цилиндра ($0
$S=2\pi \cdot r^{2} +2\pi \cdot r\cdot h$ - формула площади полной поверхности
$v=\pi \cdot r^{2} \cdot h$ - формула объема цилиндра
Выразим из формулы объема высоту:
\[v=\pi \cdot r^{2} \cdot h\Rightarrow h=\frac{v}{\pi \cdot r^{2} } \]По условию задачи, $v=25$; следовательно, $h=\frac{25}{\pi \cdot r^{2} } $.
Подставим выражение для высоты в формулу площади полной поверхности:
\[S=2\pi \cdot r^{2} +2\pi \cdot r\cdot \frac{25}{\pi \cdot r^{2} } =2\cdot \left(\pi \cdot r^{2} +\frac{25}{r} \right).\]Получаем исходную функцию: $S(r)=2\cdot \left(\pi \cdot r^{2} +\frac{25}{r} \right)$.
Производная заданной функции:
\[S'(r)=2\cdot \left(2\pi \cdot r-\frac{25}{r^{2} } \right).\] \[S'(r)=0\Rightarrow 2\cdot \left(2\pi \cdot r-\frac{25}{r^{2} } \right)=0\Rightarrow 2\pi \cdot r-\frac{25}{r^{2} } =0\Rightarrow r_{1} =\sqrt[{3}]{\frac{25}{2\pi } } .\]$r_{1} =\sqrt[{3}]{\frac{25}{2\pi } } $ - стационарная точка
Исследуем знак $S'(x)$ с помощью числовой прямой (положительная полуось):
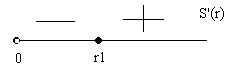
Рисунок 4.
Определим характер поведения функции
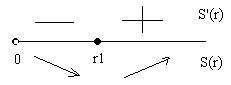
Рисунок 5.
Функция достигает минимума в точке $r_{1} =\sqrt[{3}]{\frac{25}{2\pi } } $.
Вычислим высоту цилиндра: $h=\frac{25}{\pi \cdot \left(\sqrt[{3}]{\frac{25}{2\pi } } \right)^{2} } =\frac{25}{\pi } \cdot \left(\sqrt[{3}]{\frac{2\pi }{25} } \right)^{2} =\sqrt[{3}]{\frac{4\pi ^{2} \cdot 25^{3} }{25\cdot 25\cdot \pi ^{3} } } =2\cdot \sqrt[{3}]{\frac{25}{2\pi } } $.
Следовательно, площадь полной поверхности будет минимальной при радиусе $r=\sqrt[{3}]{\frac{25}{2\pi } } $ и высоте $h=2\cdot \sqrt[{3}]{\frac{25}{2\pi } } =2r=d$ ($d$ - диаметр цилиндра).
Физика
Ядро выпущено из пушки, наклоненной к горизонту под углом $\varphi $ ($0\le \varphi \le 2\pi $), с начальной скоростью $v_{0} =10$ м/с. Рассматриваем вакуум. Дальность полета ядра определяется формулой $R=\frac{v_{0}^{2} \sin 2\varphi }{g} $ ($g=10$м/с2). Определить угол наклона пушки, при котором дальность полета будет максимальной.
Решение:
Исходная функция: $R=\frac{100\cdot \sin 2\varphi }{10} =10\cdot \sin 2\varphi $.
Производная заданной функции: $R'(\varphi )=(10\sin 2\varphi )'=20\cdot \cos 2\varphi $.
\[R'(\varphi )=0\Rightarrow 20\cdot \cos 2\varphi =0\Rightarrow \cos 2\varphi =0\Rightarrow \varphi _{1} =\frac{\pi }{4} ;\varphi _{2} =\frac{3\pi }{4} \]Исследуем знак $R'(\varphi )$ с помощью числовой прямой:
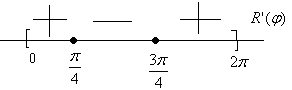
Рисунок 6.
Определим характер поведения функции
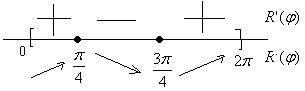
Рисунок 7.
Вычислим значения заданной функции в точках $\varphi _{1} =\frac{\pi }{4} $ и $\varphi _{2} =2\pi $.
\[R\left(\frac{\pi }{4} \right)=10\cdot \sin \left(2\cdot \frac{\pi }{4} \right)=10\cdot \sin \frac{\pi }{2} =10\] \[R\left(2\pi \right)=10\cdot \sin \left(2\cdot 2\pi \right)=10\cdot \sin 4\pi =0\]Функция достигает максимума в точке $\varphi =\frac{\pi }{4} $.
Следовательно, дальность полета ядра будет максимальной при угле наклона пушки $\varphi =\frac{\pi }{4} $.












