Формулы для вычисления работы переменной силы
Работа переменной силы $\overline{F}=P\left(x,y\right)\cdot \overline{i}+Q\left(x,y\right)\cdot \overline{j}$ по перемещению материальной точки $M\left(x,y\right)$ от точки $A$ до точки $B$ вдоль кривой $AB$ вычисляется по формуле, условно записываемой в виде $A=\int \limits _{AB}P\left(x,y\right)\cdot dx+Q\left(x,y\right)\cdot dy $.
В зависимости от формы задания кривой $AB$ этот интеграл приобретает различный вид.
- Если на некотором отрезке $\left[\alpha ,\; \beta \right]$ кривая $AB$ задана параметрически, то есть $x=x\left(t\right)$, $y=y\left(t\right)$, причем точке $A$ соответствует значение $t=\alpha $, а точці $B$~-- значення $t=\beta $, то \[A=\int \limits _{\alpha }^{\beta }P\left(x\left(t\right),y\left(t\right)\right)\cdot x'\left(t\right)\cdot dt +\int \limits _{\alpha }^{\beta }Q\left(x\left(t\right),y\left(t\right)\right)\cdot y'\left(t\right)\cdot dt .\]
- Если на некотором отрезке $\left[a,\; b\right]$ кривая $AB$ задана уравнением $y=y\left(x\right)$, то $A=\int \limits _{a}^{b}P\left(x,y\left(x\right)\right)\cdot dx +\int \limits _{a}^{b}Q\left(x,y\left(x\right)\right)\cdot y'\left(x\right)\cdot dx $.
- Если на некотором отрезке $\left[c,d\right]$ кривая $AB$ задана уравнением $x=x\left(y\right)$, то $A=\int \limits _{c}^{d}P\left(x\left(y\right),y\right)\cdot x'\left(y\right)\cdot dy +\int \limits _{c}^{d}Q\left(x\left(y\right),y\right)\cdot dy $.
На материальную точку $T\left(x,y\right)$ действует переменная сила $\overline{F}=\left(3\cdot x-2\cdot y\right)\cdot \overline{i}+4\cdot y\cdot \overline{j}$. Под действием этой силы материальная точка перемещается на отрезке $\left[6;15\right]$ от точки $M$ до точки $N$ вдоль синусоидальной кривой $y=7\cdot \sin \left(0,31\cdot x-1,57\right)+2$. Найти работу переменной силы $\overline{F}$ на криволинейном пути от точки $M$ до точки $N$. Построить графическое изображение пути от точки $M$ до точки $N$, а также векторы переменной сили $\overline{F}$ в этих точках.
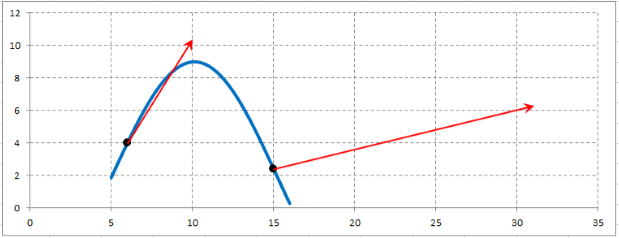
Выполняем графическое изображение синусоидальной кривой $y=7\cdot \sin \left(0,31\cdot x-1,57\right)+2$ на отрезке $\left[6;15\right]$.
Находим значения синусоиды в точках $x_{M} =6$ и $x_{N} =15$:
- $y_{M} =7\cdot \sin \left(0,31\cdot 6-1,57\right)+2\approx 4$;
- $y_{N} =7\cdot \sin \left(0,31\cdot 15-1,57\right)+2\approx 2,43$.
Выполняем графические изображения векторов переменной силы $\overline{F}=\left(3\cdot x-2\cdot y\right)\cdot \overline{i}+4\cdot y\cdot \overline{j}$, значения которого в точках $M$ и $N$ соответственно равны $\overline{F}_{M} =\left(3\cdot 6-2\cdot 4\right)\cdot \overline{i}+4\cdot 4\cdot \overline{j}=10\cdot \overline{i}+16\cdot \overline{j}$ и $\bar{F}_{N} =\left(3\cdot 15-2\cdot 2,43\right)\cdot \overline{i}+4\cdot 2,43\cdot \overline{j}=40,14\cdot \overline{i}+9,72\cdot \overline{j}$.
Работу данной силы на данном участке кривой $MN$ вычисляем по формуле $A=\int \limits _{a}^{b}P\left(x,y\left(x\right)\right)\cdot dx +\int \limits _{a}^{b}Q\left(x,y\left(x\right)\right)\cdot y'\left(x\right)\cdot dx $.
Здесь участок кривой $MN$ задан на отрезке $\left[x_{M} ,\; x_{N} \right]$, поэтому формула для работы приобретает вид: $A=\int \limits _{x_{M} }^{x_{N} }P\left(x,y\left(x\right)\right)\cdot dx +\int \limits _{x_{M} }^{x_{N} }Q\left(x,y\left(x\right)\right)\cdot y'\left(x\right)\cdot dx $.
В этой формуле первый интеграл дает значение работы силы $F$ вдоль оси $Ox$, второй интеграл -- вдоль оси $Oy$.
Находим работу силы вдоль оси $Ox$: $A_{x} =\int \limits _{6}^{15}P\left(x,y\left(x\right)\right)\cdot dx $.
Согласно условию задачи имеем:
\[P\left(x,y\right)=3\cdot x-2\cdot y; y=7\cdot \sin \left(0,31\cdot x-1,57\right)+2.\]Поэтому:
\[P\left(x,y\left(x\right)\right)=3\cdot x-2\cdot \left(7\cdot \sin \left(0,31\cdot x-1,57\right)+2\right)=\] \[=3\cdot x-14\cdot \sin \left(0,31\cdot x-1,57\right)-4.\]Далее получаем:
\[A_{x} =\int \limits _{6}^{15}\left(3\cdot x-14\cdot \sin \left(0,31\cdot x-1,57\right)-4\right)\cdot dx =\] \[=\int \limits _{6}^{15}3\cdot x\cdot dx +\int \limits _{6}^{15}\left(-14\cdot \sin \left(0,31\cdot x-1,57\right)\right)\cdot dx +\int \limits _{6}^{15}\left(-4\right)\cdot dx =\] \[=3\cdot \int \limits _{6}^{15}x\cdot dx -14\cdot \int \limits _{6}^{15}\sin \left(0,31\cdot x-1,57\right)\cdot dx -4\cdot \int \limits _{6}^{15}dx =\] \[=3\cdot \left[\frac{x^{2} }{2} \right]_{6}^{15} -14\cdot \left[-\frac{1}{0,31} \cdot \cos \left(0,31\cdot x-1,57\right)\right]_{6}^{15} -4\cdot \left[x\right]_{6}^{15} =\] \[=1,5\cdot \left(15^{2} -6^{2} \right)+\frac{14}{0,31} \cdot \left(\cos \left(0,31\cdot 15-1,57\right)-\cos \left(0,31\cdot 6-1,57\right)\right)-\] \[-4\cdot \left(15-6\right)=135,15.\]Находим работу силы вдоль оси $Oy$: $A_{y} =\int \limits _{6}^{15}Q\left(x,y\left(x\right)\right)\cdot y'\cdot dx $.
Согласно условию задачи имеем:
\[Q\left(x,y\right)=4\cdot y; y=7\cdot \sin \left(0,31\cdot x-1,57\right)+2. \]Поэтому:
\[Q\left(x,y\left(x\right)\right)=4\cdot \left(7\cdot \sin \left(0,31\cdot x-1,57\right)+2\right)=28\cdot \sin \left(0,31\cdot x-1,57\right)+8;\] \[y'=7\cdot 0,31\cdot \cos \left(0,31\cdot x-1,57\right)=2,17\cdot \cos \left(0,31\cdot x-1,57\right).\]Далее получаем:
\[A_{y} =\int \limits _{6}^{15}\left(28\cdot \sin \left(0,31\cdot x-1,57\right)+8\right)\cdot 2,17\cdot \cos \left(0,31\cdot x-1,57\right)\cdot dx =\] \[=\int \limits _{6}^{15}28\cdot 2,17\cdot \sin \left(0,31\cdot x-1,57\right)\cdot \cos \left(0,31\cdot x-1,57\right)\cdot dx +\] \[+\int \limits _{6}^{15}8\cdot 2,17\cdot \cos \left(0,31\cdot x-1,57\right)\cdot dx =\] \[=\int \limits _{6}^{15}60,76\cdot \sin \left(0,31\cdot x-1,57\right)\cdot \cos \left(0,31\cdot x-1,57\right)\cdot dx +\] \[+\int \limits _{6}^{15}17,36\cdot \cos \left(0,31\cdot x-1,57\right)\cdot dx .\]Вычисляем первый интеграл $I_{1} $:
\[I_{1} =60,76\cdot \int \limits _{6}^{15}\sin \left(0,31\cdot x-1,57\right)\cdot \cos \left(0,31\cdot x-1,57\right)\cdot dx =\] \[=60,76\cdot \frac{1}{0,31} \cdot \int \limits _{6}^{15}\sin \left(0,31\cdot x-1,57\right)\cdot d\left(\sin \left(0,31\cdot x-1,57\right)\right) =\] \[=196\cdot \left[\frac{\sin ^{2} \left(0,31\cdot x-1,57\right)}{2} \right]_{6}^{15} =\] \[=98\cdot \left(\sin ^{2} \left(0,31\cdot 15-1,57\right)-\sin ^{2} \left(0,31\cdot 6-1,57\right)\right)\approx -7,64.\]Вычисляем второй интеграл $I_{2} $:
\[I_{2} =17,36\cdot \int \limits _{6}^{15}\cos \left(0,31\cdot x-1,57\right)\cdot dx =\] \[=17,36\cdot \frac{1}{0,31} \cdot \left[\sin \left(0,31\cdot x-1,57\right)\right]_{6}^{15} =\] \[=56\cdot \left(\sin \left(0,31\cdot 15-1,57\right)-\sin \left(0,31\cdot 6-1,57\right)\right)\approx -12,57.\]Работа силы вдоль оси $Oy$:
\[A_{y} =I_{1} +I_{2} =-7,64-12,57=-20,21.\]Общая работа силы при перемещении вдоль кривой:
\[A=A_{x} +A_{y} =135,15-20,21=114,94.\]











