Вычислить площадь фигуры, ограниченной линиями $y=x^{2} +2\cdot x$ и $y=x+2$.
Решение.
Графическое изображение фигуры:
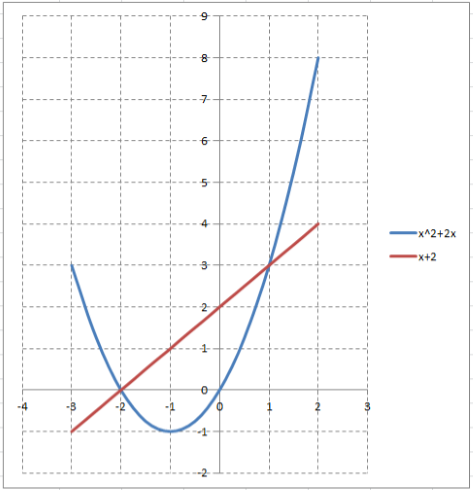
Точки пересечения линий определяем как результат совместного решения их уравнений:
\[x^{2} +2\cdot x=x+2; x^{2} +x-2=0; x_{1} =-2; x_{2} =1. \]Поскольку прямая находится выше параболы, то площадь фигуры вычисляем следующим образом:
\[S=\int \limits _{-2}^{1}\left(\left(x+2\right)-\left(x^{2} +2\cdot x\right)\right)\cdot dx =\int \limits _{-2}^{1}\left(-x^{2} -x+2\right)\cdot dx ;\] \[\int \left(-x^{2} -x+2\right)\cdot dx =-\int x^{2} \cdot dx -\int x\cdot dx +2\cdot \int dx =-\frac{x^{3} }{3} -\frac{x^{2} }{2} +2\cdot x;\] \[S=\left[-\frac{x^{3} }{3} -\frac{x^{2} }{2} +2\cdot x\right]_{-2}^{1} =\left(-\frac{1^{3} }{3} -\frac{1^{2} }{2} +2\cdot 1\right)-\left(-\frac{\left(-2\right)^{3} }{3} -\frac{\left(-2\right)^{2} }{2} +2\cdot \left(-2\right)\right)=\]$=\left(-\frac{1}{3} -\frac{1}{2} +2\right)-\left(\frac{8}{3} -2-4\right)=\frac{7}{6} +\frac{10}{3} =\frac{9}{2} $ кв.ед.
Вычислить площадь фигуры, ограниченной линиями $y=x^{2} -6$, $y=-x^{2} $.
Решение.
Графическое изображение фигуры:
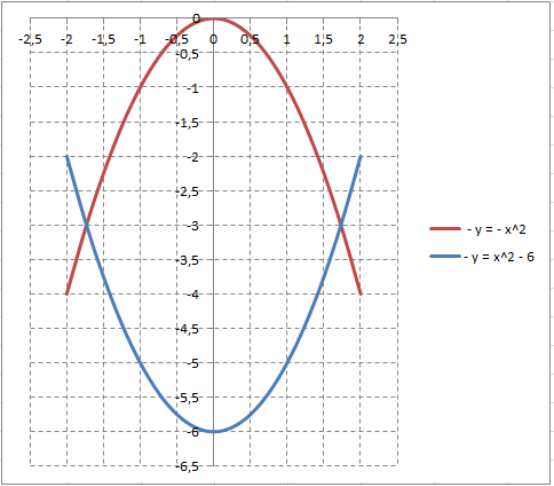
Точки пересечения линий определяем как результат совместного решения их уравнений:
\[x^{2} -6=-x^{2} ; 2\cdot x^{2} =6; x_{1} =-\sqrt{3} ; x_{2} =\sqrt{3} . \]Поскольку вторая парабола находится выше первой, то площадь фигуры вычисляем следующим образом:
\[S=\int \limits _{-\sqrt{3} }^{\sqrt{3} }\left(\left(-x^{2} \right)-\left(x^{2} -6\right)\right)\cdot dx =\int \limits _{-\sqrt{3} }^{\sqrt{3} }\left(-2\cdot x^{2} +6\right)\cdot dx =\] \[=-2\cdot \int \limits _{-\sqrt{3} }^{\sqrt{3} }x^{2} \cdot dx +6\cdot \int \limits _{-\sqrt{3} }^{\sqrt{3} }dx =-\frac{2}{3} \cdot \left[x^{3} \right]_{-\sqrt{3} }^{\sqrt{3} } +6\cdot \left[x\right]_{-\sqrt{3} }^{\sqrt{3} } =\]$=-\frac{2}{3} \cdot \left(3\cdot \sqrt{3} +3\cdot \sqrt{3} \right)+6\cdot \left(\sqrt{3} +\sqrt{3} \right)=8\cdot \sqrt{3} $ кв.ед.
Вычислить площадь фигуры, ограниченной линиями $y=x^{2} -5\cdot x+4$ и $y=2-2\cdot x$.
Решение.
Графическое изображение фигуры:
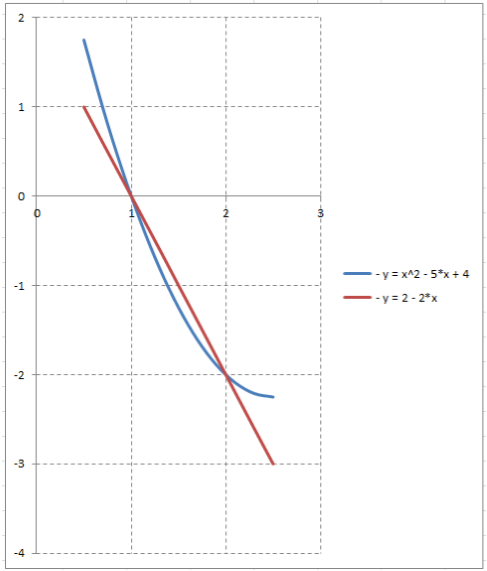
Точки пересечения линий определяем как результат совместного решения их уравнений:
\[x^{2} -5\cdot x+4=2-2\cdot x; x^{2} -3\cdot x+2=0; x_{1} =1; x_{2} =2. \]Поскольку прямая находится выше параболы, то площадь фигуры вычисляем следующим образом:
\[S=\int \limits _{1}^{2}\left(\left(2-2\cdot x\right)-\left(x^{2} -5\cdot x+4\right)\right)\cdot dx =\int \limits _{1}^{2}\left(-x^{2} +3\cdot x-2\right)\cdot dx =\] \[=\left[-\frac{x^{3} }{3} +3\cdot \frac{x^{2} }{2} -2\cdot x\right]_{1}^{2} =\left(-\frac{2^{3} }{3} +3\cdot \frac{2^{2} }{2} -2\cdot 2\right)-\left(-\frac{1^{3} }{3} +3\cdot \frac{1^{2} }{2} -2\cdot 1\right)=\]$=-\frac{8}{3} +3\cdot 2-2\cdot 2+\frac{1}{3} -\frac{3}{2} +2=-\frac{7}{3} -\frac{3}{2} +4=\frac{1}{6} $ кв.ед.
Вычислить площадь фигуры, ограниченной линиями $y=x$, $y=x^{2} $, $y=-2\cdot x+3$.
Решение.
Графическое изображение фигуры:
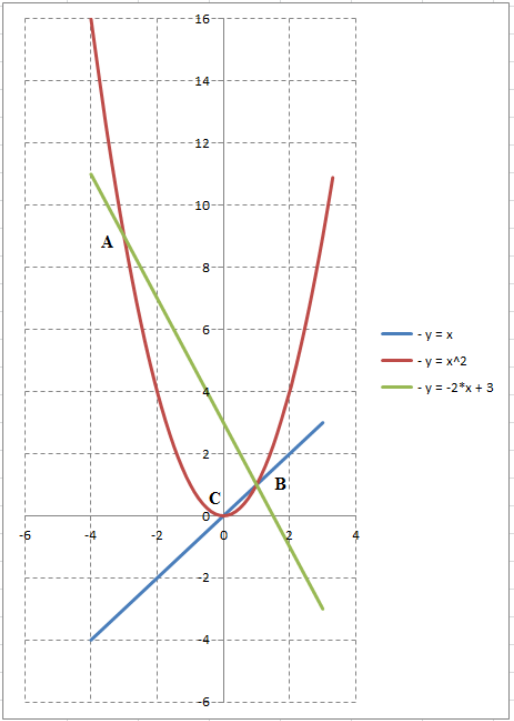
Фигура $ABC$ образована следующим образом:
- точка $A$ -- пересечение кривых $y=x^{2} $ и $y=-2\cdot x+3$; координаты точек пересечения определяются из уравнения $x^{2} =-2\cdot x+3$; получаем $x_{A} =-3$, $x_{B} =1$;
- точка $B$ -- пересечение всех трех кривых; координаты точки $x_{B} =1$;
- точка $C$ -- пересечение кривых $y=x^{2} $ и $y=x$; координаты точек пересечения определяются из уравнения $x^{2} =x$; получаем $x_{C} =0$, $x_{B} =1$.
Таким образом, площадь фигуры $ABC$ можно представить состоящей из двух частей:
\[S=\int \limits _{-3}^{0}\left(\left(-2\cdot x+3\right)-\left(x^{2} \right)\right)\cdot dx +\int \limits _{0}^{1}\left(\left(-2\cdot x+3\right)-\left(x\right)\right)\cdot dx =\] \[=\int \limits _{-3}^{0}\left(-x^{2} -2\cdot x+3\right)\cdot dx +\int \limits _{0}^{1}\left(-3\cdot x+3\right)\cdot dx =\] \[=\left[-\frac{x^{3} }{3} -2\cdot \frac{x^{2} }{2} +3\cdot x\right]_{-3}^{0} +\left[-3\cdot \frac{x^{2} }{2} +3\cdot x\right]_{0}^{1} =\] \[=-\left(-\frac{\left(-3\right)^{3} }{3} -2\cdot \frac{\left(-3\right)^{2} }{2} +3\cdot \left(-3\right)\right)+\left(-3\cdot \frac{1^{2} }{2} +3\cdot 1\right)=\]$=-9+9+9-\frac{3}{2} +3=\frac{21}{2} $ кв.ед.












