Найти объем тела, образованного вращением (ОТВ) вокруг оси $Ox$ плоской фигуры, ограниченной сверху параболой $y_{1} =-2\cdot x^{2} +16\cdot x+18$, снизу -- параболой $y_{2} =2\cdot x^{2} -8\cdot x+18$, а слева и справа прямыми $x=1$ и $x=5$ соответственно.
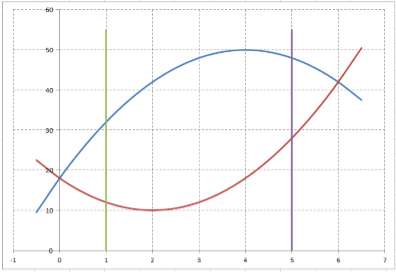
Выполняем графические построения:
 тела вращения и площадь поверхности тела вращения">
тела вращения и площадь поверхности тела вращения">
При вращении этой плоской фигуры вокруг оси $Ox$ верхняя парабола (обозначенная синим цветом) образует общий объем, а нижняя парабола (обозначенная оранжевым цветом) образует отверстие. Таким образом, ОТВ вычисляется как разность общего объема и объема отверстия.
Известно, что ОТВ (вокруг оси $Ox$) вычисляется по формуле $V=\pi \cdot \int \limits _{a}^{b}y^{2} \left(x\right)\cdot dx $, где $y=y\left(x\right)$ -- неотрицательная непрерывная функция, образующая криволинейную трапецию на отрезке $\left[a,\; b\right]$.
Общий объем будем вычислять по формуле $V_{1} =\pi \cdot \int \limits _{1}^{5}y_{1}^{2} \cdot dx $.
Получаем:
\[V_{1} =\pi \cdot \int \limits _{1}^{5}\left(-2\cdot x^{2} +16\cdot x+18\right)^{2} \cdot dx =\] \[=\pi \cdot \int \limits _{1}^{5}\left(\left(-2\cdot x^{2} \right)^{2} +\left(16\cdot x\right)^{2} +\left(18\right)^{2} +2\cdot \left(-2\cdot x^{2} \right)\cdot \left(16\cdot x\right)+\right. \] \[\left. +2\cdot \left(-2\cdot x^{2} \right)\cdot 18+2\cdot \left(16\cdot x\right)\cdot 18\right)\cdot dx=\] \[=\pi \cdot \int \limits _{1}^{5}\left(4\cdot x^{4} -64\cdot x^{3} +184\cdot x^{2} +576\cdot x+324\right)\cdot dx =\] \[=\pi \cdot \left(4\cdot \int \limits _{1}^{5}x^{4} \cdot dx -64\cdot \int \limits _{1}^{5}x^{3} \cdot dx +184\cdot \int \limits _{1}^{5}x^{2} \cdot dx +576\cdot \int \limits _{1}^{5}x\cdot dx +324\cdot \int \limits _{1}^{5}dx \right)=\] \[=\pi \cdot \left(4\cdot \left[\frac{x^{5} }{5} \right]_{1}^{5} -64\cdot \left[\frac{x^{4} }{4} \right]_{1}^{5} +184\cdot \left[\frac{x^{3} }{3} \right]_{1}^{5} +576\cdot \left[\frac{x^{2} }{2} \right]_{1}^{5} +324\cdot \left[x\right]_{1}^{5} \right)=\] \[=\pi \cdot \left(4\cdot \frac{1}{5} \cdot \left(5^{5} -1^{5} \right)-64\cdot \frac{1}{4} \cdot \left(5^{4} -1^{4} \right)+184\cdot \frac{1}{3} \cdot \left(5^{3} -1^{3} \right)+\right. \] \[\left. +576\cdot \frac{1}{2} \cdot \left(5^{2} -1^{2} \right)+324\cdot \left(5-1\right)\right)=\] \[=\pi \cdot \left(4\cdot \frac{1}{5} \cdot 3124-64\cdot \frac{1}{4} \cdot 624+184\cdot \frac{1}{3} \cdot 124+576\cdot \frac{1}{2} \cdot 24+324\cdot 4\right)=\] \[=\pi \cdot \left(2499,2-9984+7605,3+6912+1296\right)=\pi \cdot 8328,5\approx 26151,5.\]Аналогичным образом находим объем отверстия:
\[V_{2} =\pi \cdot \int \limits _{1}^{5}y_{2} ^{2} \cdot dx =\pi \cdot \int \limits _{1}^{5}\left(2\cdot x^{2} -8\cdot x+18\right)^{2} \cdot dx .\]Теперь вычисляем объем тела: $V=V_{1} -V_{2} $.
Вычислить ОТВ, образованного вращением вокруг оси $Ox$ фигуры, ограниченной линиями $y=x^{4} $ и $y=x$.
Графическое изображение фигуры:
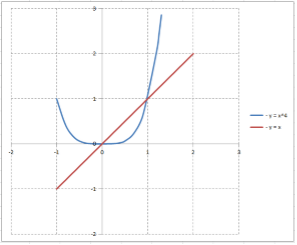
Решив совместно уравнения $y=x^{4} $ и $y=x$, получим $x_{1} =0$ и $x_{2} =1$ -- этими прямыми фигура ограничена слева и справа.
Искомый объем определяется как разность объемов, полученных в результате вращения вокруг оси $Ox$ двух криволинейных трапеций: первая ограничена прямой $y_{1} =x$, вторая -- параболой $y_{2} =x^{4} $.
ОТВ, образованного вращением вокруг оси $Ox$ криволинейной трапеции, ограниченной сверху кривой $y=y_{1} \left(x\right)$, снизу -- кривой $y=y_{2} \left(x\right)$, а также двумя прямыми $x=a$ и $x=b$ слева и справа, будем вычислять по формуле $V=\pi \cdot \int \limits _{a}^{b}\left(y_{1}^{2} -y_{2}^{2} \right)\cdot dx $.
Имеем:
\[V=\pi \cdot \int \limits _{0}^{1}\left(\left(x\right)^{2} -\left(x^{4} \right)^{2} \right)\cdot dx =\pi \cdot \left[\frac{x^{3} }{3} -\frac{x^{9} }{9} \right]_{0}^{1} =\pi \cdot \left(\frac{1}{3} -\frac{1}{9} \right)=\pi \cdot \frac{2}{9} .\]Зайти площадь поверхности, образованной вращением вокруг оси $Ox$ кривої $y=\sqrt{80\cdot x+15} $ между точками з абсцисами $x=3$ и $x=13$.
Графическое изображение вращаемой кривой:
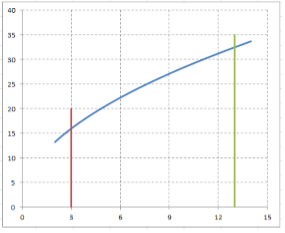
Площадь поверхности тела вращения выражается формулой $Q=2\cdot \pi \cdot \int \limits _{a}^{b}y\cdot \sqrt{1+y'^{2} } \cdot dx $, где $y=y\left(x\right)$ -- неотрицательная функция, заданная на отрезке $\left[a,\; b\right]$.
Находим выражение $\sqrt{1+y'^{2} } $:
\[y'=\frac{80}{2\cdot \sqrt{80\cdot x+15} } ;\] \[\sqrt{1+y'^{2} } =\sqrt{1+\frac{80^{2} }{4\cdot \left(80\cdot x+15\right)} } =\frac{1}{2} \cdot \sqrt{\frac{320\cdot x+6460}{80\cdot x+15} } .\]Находим выражение для подынтегральной функции $y\cdot \sqrt{1+y'^{2} } $:
\[\sqrt{80\cdot x+15} \cdot \frac{1}{2} \cdot \sqrt{\frac{320\cdot x+6460}{80\cdot x+15} } =\frac{1}{2} \cdot \sqrt{320\cdot x+6460} .\]Записываем интеграл и вычисляем площадь поверхности:
\[Q=\pi \cdot \int \limits _{3}^{13}\sqrt{320\cdot x+6460} \cdot dx =\] \[=\pi \cdot \left[\frac{1}{320} \cdot \frac{\left(320\cdot x+6460\right)^{\frac{1}{2} +1} }{\frac{1}{2} +1} \right]_{3}^{13} =\pi \cdot \left[\frac{1}{480} \cdot \left(320\cdot x+6460\right)^{\frac{3}{2} } \right]_{3}^{13} =\] \[=\frac{\pi }{480} \cdot \left[\left(320\cdot x+6460\right)\cdot \sqrt{320\cdot x+6460} \right]_{3}^{13} =\] \[=\frac{\pi }{480} \cdot \left(\left(320\cdot 13+6460\right)\cdot \sqrt{320\cdot 13+6460} -\right. \] \[\left. -\left(320\cdot 3+6460\right)\cdot \sqrt{320\cdot 3+6460} \right)=\] \[=\frac{\pi }{480} \cdot \left(10620\cdot \sqrt{10620} -7420\cdot \sqrt{7420} \right)\approx \] \[\approx \frac{3,14}{480} \cdot \left(10620\cdot 103,053-7420\cdot 86,139\right)\approx \]$\approx \frac{3,14}{480} \cdot \left(1094423-639151\right)\approx \frac{3,14}{480} \cdot 455272\approx 2978$ кв.од.











