В различных явлениях некоторые величины изменяются, а другие сохраняют свое числовое значение. Например, при равномерном движении точки время и расстояние меняются, а скорость остается постоянной.
В связи с этим, все анализируемые и вычисляемые величины принято разделять на постоянные и переменные.
Что такое постоянная величина
Постоянная величина принимает равновозможные значения, в то время как переменная -- характеризуется своим непостоянством и принимает различные значения. В математике постоянная величина часто рассматривается как частный случай переменной, у которой все числовые значения одинаковы.
Рассмотрим несколько примеров:
- Пусть в равнобедренный треугольник вписано n окружности диаметров: x1,x2,..xn
- Рассмотрим накопительную величину сумм диаметров вписанных окружностей.
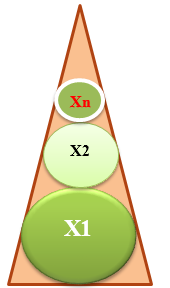
Рисунок 1. Пример переменной величины
Диаметр конечной окружности является величиной переменной! Чем больше число вписанных в треугольник окружностей, тем меньше радиус последней из них, т.е. при n $\to \infty $, x $\to 0.$
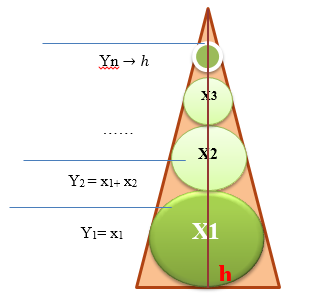
Рисунок 2. Пример переменной величины
Из рисунка 2 видно, что чем больше окружностей вписано, тем более вероятно приближение величины Y(сумма диаметров) к величине h:
При n $\to \infty $, y $\to h$
Число а называют пределом переменной величины х, если в процессе изменения х неограниченно приближается к а.
\[\lim x=a\]Опираясь на определение, можно сказать, что пределом переменной величины xn является число 0 для примера 1, и число h для величины Yn в примере 2.
\[\mathop{\lim x_{n} }\limits_{n\to \infty } =0\] \[\mathop{\lim Y_{n} }\limits_{n\to \infty } =h\]Множество всех числовых значений переменной величины лежит на области изменения самой переменной.
Что такое упорядоченные переменные величины
Переменные величины называют упорядоченными, если область изменения переменной х равна:
\[x_{n} =\frac{1}{n} \]Частным случаем упорядоченной переменной величины является переменная величина, значения которой образуют числовую последовательность $x_1,x_2,\dots , x_n$. Для таких величин значение $x_i$ считается предшествующим, а $x_j$ -- последующим независимо от того, какое из этих значений больше. Таким образом, числовая последовательность -- это переменная величина, последовательные значения которой могут быть перенумерованы.
Постоянное число а называется пределом переменной величины х, если для каждого наперед заданного произвольно малого положительного числа ${\mathbf \varepsilon }$ можно указать такое значение переменной х, что все последующие значения переменной будут удовлетворять неравенству
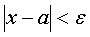
Предел постоянной всегда равен самой постоянной:
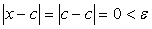
Переменная величина не может иметь двух пределов
Пусть переменная величина х, в процессе изменения неограниченно приближается к числу 8, принимая значение: 7,9; 7,99; 7,999 и т.д. В этом случае модуль разности:
\[\left|E-0\right|=0,1;0,01;0,001\]По определению 2, число 8 -- предел переменной величины.
\[\mathop{\lim x}\limits_{} =8\]Предел переменной величины, учитывая наличие заданного произвольно малого положительного числа, можно изобразить следующим образом:
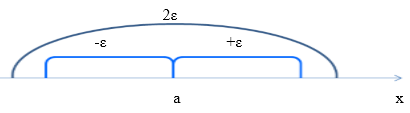
Рисунок 3. Окрестность точки а











