Функция y=f(x) называется ограниченной на некотором множестве М значений аргумента х, если существует такое положительное число С, что при всех x$\in $M выполняется неравенство:
\[\left|f(x)\right|\le C\]Таким множеством может быть, например, интервал, отрезок или же вся числовая прямая.
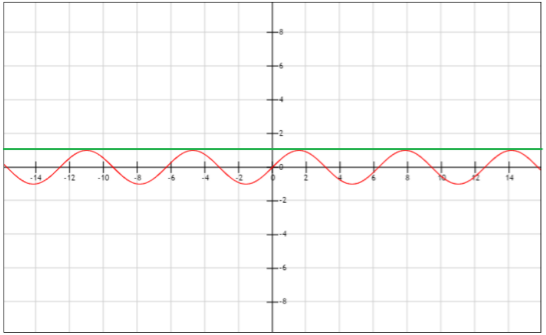
Функция y=sin(x) ограничена на всей числовой прямой, так как для любого значения х имеем $ |sin x|≤ 1$.
 Ограниченная функция">
Ограниченная функция">
Рисунок 1. Ограниченная функция
Функция y = x3 + 4 ограничена на отрезке [0, 3], так как для всех х, принадлежащих этому отрезку, имеет место неравенство:
\[\left|f(x)\right|\le f(3)=31\]Данное неравенство получается вследствие подстановки числа 3 вместо х функции:
y = 33 + 4 = 27 + 4 = 31
Значит |f(x)| ≤ 31.
Является ли функция $y=\frac{1}{x} $ ограниченной на интервале (0, 1)?
Ответ: Поскольку нельзя указать такое число С, чтобы при всех x$\in $(0,1) выполнялось неравенство:
\[\frac{1}{x} \le C\]Функция не является ограниченной.
Если функция y=f(x) имеет предел при $x\to +\infty$, то она ограничена на некотором бесконечном интервале $(N,+ \infty)$.
Пусть,
\[\mathop{\lim }\limits_{x\to +\infty } f(x)=b\]Тогда, согласно определению предела, для $\varepsilon $ = 1 имеем
\[\exists N\mathop{\forall }\limits_{x} (x>N)\Rightarrow \left|f(x)-b\right|Но по свойству абсолютных величин, выполняется неравенство: $\left|f(x)-b\right|\ge \left|f(x)\right|-b$, поэтому $\left|f(x)-b\right|А значит, \[\left|f(x)\right|В связи с чем можно сделать вывод, что функция y=f(x) ограничена на бесконечном интервале $(N,+ \infty)$.Функция, ограниченная на бесконечном интервале $(N,+ \infty)$, называется ограниченной при $x\to +\infty$.
Если функция y=f(x) имеет предел, отличный от нуля (при $x\to +\infty$), то функция
\[y=\frac{1}{f(x)} \]ограничена (на некотором бесконечном интервале).
Пусть,
\[\mathop{\lim }\limits_{x\to +\infty } f(x)=b,(b\ne 0)\]И пусть задано положительное число $\varepsilon \[\exists N\mathop{\forall }\limits_{x} (x>N)\Rightarrow \left|f(x)-b\right|Так как:
$\left|f(x)-b\right|=\left|b-f(x)\right|\ge \left|b\right|-\left|f(x)\right|$, то $\left|b\right|-\left|f(x)\right|\left|b\right|-\varepsilon >0$А значит,
\[\left|\frac{1}{f(x)} \right|=\frac{1}{\left|f(x)\right|}











