Числовой последовательностью называется функция $a_n= f(n)$ натурального аргумента n.
$n = x_1, x_2, x_3 \dots x_i$
Числа $x_1, x_2, x_3 \dots x_i$ являются членами числовой последовательности
Например,
n = -2, 0, 2, 4
где,
-2 -- первый член последовательности;
0 -- второй член последовательности;
2 -- третий член последовательности;
4 -- четвертый член последовательности.
Кратно, числовая последовательность записывается в виде:
$a_n= f(n) или \{a_n \}$
Числовая последовательность -- функция, область определения которой есть множество N всех натуральных чисел. Совокупность таких чисел an называют множеством значений последовательности.
Написать последовательность всех четных неотрицательных чисел
$2,4,6,8\dots $
Словестно описать последовательность вида: $0,5,10,15,20 \dots$
Ответ: дана последовательность неотрицательных, кратных 5 чисел.
2. Аналитический -- с помощью формулы
Вычислить первые три члена последовательности
$a_n=4*(n-1)$
Решение:
$a1 = 4*(n-1) = 4*(1-1) = 0$
$a2 = 4*(n-1) = 4*(2-1) = 4$
$a3 = 4*(n-1) = 4*(3-1) = 8$
Привести аналитический вид последовательности вида: $1,4,7 \dots$
Решение:
4 = 3+1
7 = 4+3
Значит, числовая последовательность имеет вид: $a_n = 3n-2$
3. Реккурентный способ для вычисления следующего члена последовательности использует в своей формуле значения ее предыдущего члена.
Записать первые три члена последовательности $a_n$, если $а_1 = 2, а_{n+1} = 4 + а_n$
Решение:
а1 = 2
а2 = 4 + 2 = 6
а3 = 6 + 2 = 8
Ответ: 2,6,8
4. Графический. Числовая последовательность определяется с помощью графика на котором изображены отдельные точки, абсциссы которых являются членами числовой последовательности, а ординаты - порядковым номером членов последовательности.
По графику, изображенному на рисунке 1, записать числовую последовательность.
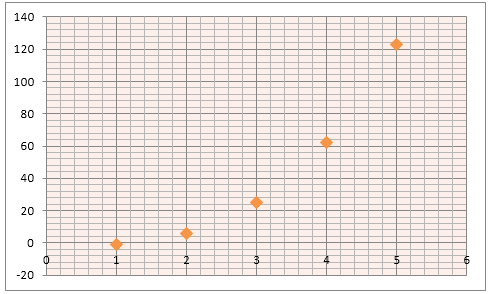
Рисунок 1. Графическое определение последовательности
Решение:
Выпишем координаты каждой точки изображенной на графике:
(1;0) (2;2) (3;5) (4;4) (5;2)
Получим:
а1 = 0, а2 = 2, а3 = 5, а4 = 4, а5 = 2
Данная числовая последовательность состоит из 5 членов, поэтому ее можно назвать -- конечной числовой последовательностью.
Если числовая последовательность в качестве функции будет задана на всем множестве натуральных чисел, то такая последовательность будет бесконечной числовой последовательностью.
Числовую последовательность называют возрастающей, если ее члены возрастают ($a_{n+1} > a_n$), и убывающей, если ее члены убывают ($a_{n+1} > a_n$).
Например,
1, 3, 8 -- возрастающая последовательность
7, 5, 3, 1 -- убывающая последовательность
Возрастающая или убывающая числовые последовательности называются монотонными.
Действия с последовательностями
- Умножение на число \[a\left\{x_{n} \right\}=\left\{ax_{1} ,ax_{2} ...ax_{n} ,\right\}=\left\{ax_{n} \right\}\]
- Сложение и вычитание \[\left\{x_{n} \right\}\pm \left\{y_{n} \right\}=\left\{x_{1} \pm y_{1} ,x_{2} \pm y_{2} ...x_{n} \pm y_{n} ,\right\}=\left\{x_{n} \pm y_{n} \right\}\]
- Произведение \[\left\{x_{n} \right\}\cdot \left\{y_{n} \right\}=\left\{x_{1} \cdot y_{1} ,x_{2} \cdot y_{2} ...x_{n} \cdot y_{n} ,\right\}=\left\{x_{n} \cdot y_{n} \right\}\]
- Частное \[\left\{x_{n} \right\}/\left\{y_{n} \right\}=\left\{x_{1} /y_{1} ,x_{2} /y_{2} ...x_{n} /y_{n} ,\right\}=\left\{x_{n} /y_{n} \right\}\]












