Основные понятия
При вычислении вероятностей событий по формуле Бернулли иногда необходимо не только вычислить эти значения, но и суммировать их, причем число слагаемых в этой сумме может быть значительным. В этом случае используют интегральную теорему Муавра -- Лапласа.
Пусть в испытаниях Бернулли вероятность появления события равна p ($0 \[P(a \le \frac{k-n \cdot p}{\sqrt{n\cdot p\cdot q} } Где
\[\varphi (x)=\frac{1}{\sqrt{2\pi } } \cdot e^{-x^{2} /2} .\]Для практических расчетов будем использовать приближенное равенство
\[P_{n} (k_{1} ,k_{2} )=P(k_{1} \le k\le k_{2} )\approx \Phi \left(\frac{k_{2} -n\cdot p}{\sqrt{n\cdot p\cdot q} } \right)-\Phi \left(\frac{k_{1} -n\cdot p}{\sqrt{n\cdot p\cdot q} } \right),\]где $0\le k_{1} \[\Phi (x)=\frac{1}{\sqrt{2\pi } } \int \limits _{-\infty }^{x}\exp (-t^{2} /2)dt .\]
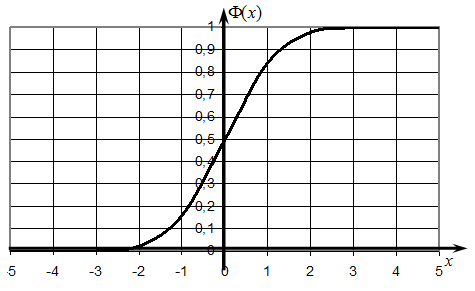
Построим график функции $\Phi (x)$ (см. рис.).
 испытаниях">
испытаниях">
Будем считать для $E > 3,5$ $\Phi (x)\approx 1$, для $E \[\Phi (x)+\Phi (-x)=1.\]
Пусть в испытаниях Бернулли $\mu$ - число появления события A в n испытаниях. Обозначим через $\frac{\mu }{n} $ частоту появления события A. Оценим вероятность$P\left(\left|\frac{\mu }{n} -p\right|$0. Воспользуемся интегральной теоремой Муавра -- Лапласа:
\[P_{n} (k_{1} ,k_{2} )=P(k_{1} \le k\le k_{2} )=P\left(\frac{k_{1} -n\cdot p}{\sqrt{n\cdot p\cdot q} } \le \frac{k-n\cdot p}{\sqrt{n\cdot p\cdot q} } \le \frac{k_{2} -n\cdot p}{\sqrt{n\cdot p\cdot q} } \right)\approx \] \[\approx \Phi \left(\frac{k_{2} -n\cdot p}{\sqrt{n\cdot p\cdot q} } \right)-\Phi \left(\frac{k_{1} -n\cdot p}{\sqrt{n\cdot p\cdot q} } \right).\]Имеем
\[P\left(\left|\frac{\mu }{n} -p\right|Таким образом искомая оценка имеет вид \[P\left(\left|\frac{\mu }{n} -p\right|Полученное трансцендентное уравнение всегда имеет единственное решение, если известны значения всех параметров кроме одного. Этим фактом подтверждается многочисленные применения интегральной теоремы Муавра-Лапласа.Применение к решению задач
Вероятность появления события в каждом из независимых испытаний равна 0,5. Найти число испытаний n, при котором с вероятностью $\gamma$=0,7698 можно ожидать, что относительная частота появления события отклонится от его вероятности по абсолютной величине не более чем на 0,02.
Решение.
Из условия задачи можно увидеть, что имеет место схема испытаний Бернулли с $p=0,5$, $q=1-p=1-0,5=0,5$. Найдем число испытаний n, при котором с вероятностью $\gamma =0,7698$ можно ожидать, что относительная частота $\frac{\mu }{n} $ появления события отклонится от его вероятности $p=1/2$ по абсолютной величине не более чем на $\varepsilon =0,02$. Имеем цепочку равенств
\[P\left(\left|\frac{\mu }{n} -p\right|Вероятность выхода из строя во время проведения эксперимента, который имеет в виду обнаружить надежность устройства в работе, равняется 0,2. Было проверено 625 устройств. Чему равняется вероятность, того, что абсолютная величина отклонения относительной частоты выхода из строя устройств от вероятности p=0,2 становит 0,02?
Решение.
По условию задачи n=625; p=0,2; q=1-p; $\epsilon$=0,02. Подставив эти значения в выведеную формулу:
\[P\left(\left|\frac{\mu }{n} -p\right|получим: \[P\left(\left|\frac{\mu }{625} -0,2\right|













