Обратная пропорциональность

Источник статьи

Автор24 — учеба по твоим правилам

Определение 1

Обратной пропорциональностью называется функция, которую можно задать формулой вида: $y=\frac{k}{x}$ , где $x$ - независимая переменная, $k$ - не равное нулю число.

Определение 2

Графиком обратной пропорциональности является кривая, состоящая из двух ветвей, которая называется гипербола.

Пример 1

Построить график функции $y= \frac{1}{x}$

Для построения графика сначала определим значения, которые может принимать независимая переменная $x.$

Как вы видите, значения функции будут определены для всех $x$ , кроме $x=0$ ,значит допустимы все значения независимой переменной, кроме $0$ .

Далее для построения графика мы будем последовательно придавать аргументу несколько значений и вычислять соответствующие значения зависимой переменной $y$ .

При $x=1$ $y=1$

При $x=2$ $y=0,5$ , при $x= 0,5$ $y=2$

При $x=4$ $y =0,25$ , при $x=0,25$ $y= 4$

При $x=8$ $y=0,125$ , при $x=0,125$ $y=8$

При $x=2$ $y=0,5$ , при $x= 0,5$ $y=2$

При $x=4$ $y =0,25$ , при $x=0,25$ $y= 4$

При $x=8$ $y=0,125$ , при $x=0,125$ $y=8$

При $x= -1$ $y= -1$

При $x= -2$ $y= -0,5$ , при $x= -0,5$ $y= -2$

При $x= -4$ $y = -0,25$ , при $x= -0,25$ $y= -4$

При $x= -8$ $y= -0,125$ , при $x= -0,125$ $y= -8$

При $x= -2$ $y= -0,5$ , при $x= -0,5$ $y= -2$

При $x= -4$ $y = -0,25$ , при $= -0,25$ $у= -4$

При $x= -8$ $y= -0,125$ , при $x= -0,125$ $y= -8$

Теперь обратим внимание, что при положительных значениях независимой переменной функция принимает положительные значения, при отрицательных - отрицательные, т.е график будет расположен в I и III координатных четвертях, при этом не будет проходить через начало координат.

Нанесем полученные координаты на координатную плоскость, последовательно их соединим и получим график функции, который изображен ниже схематично:

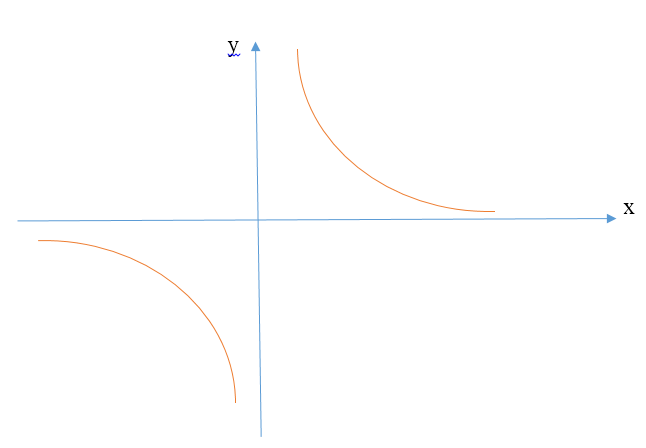
Рисунок 1.

Пример 2

Построить график функции $y= -\frac{1}{x}$

Аналогично предыдущему примеру, обратим внимание, что для независимой переменной $x$ допустимы все значения, кроме $0$ .

Снова будем последовательно придавать аргументу несколько значений и вычислять соответствующие значения зависимой переменной $y$ .

При $x= 1$ $y= -1$

При $x= 2$ $y= -0,5$ , при $x= 0,5$ $y= -2$

При $x= 4$ $y = -0,25$ , при $x= 0,25$ $y= -4$

При $x= 8$ $y= -0,125$ , при $x= 0,125$ $y= -8$

При $x= -1$ $y=1$

При $x= -2$ $y= 0,5$ , при $x= -0,5$ $y= 2$

При $x= -4$ $y = 0,25$ , при $x=- 0,25$ $y= 4$

При $x= -8$ $y= 0,125$ , при $x= -0,125$ $y=8$

В данной функции видим, что при положительных значениях независимой переменной функция принимает отрицательные значения, при отрицательных-положительные, т.е. график будет расположен во II и IV координатных четвертях, при этом не будет проходить через начало координат.

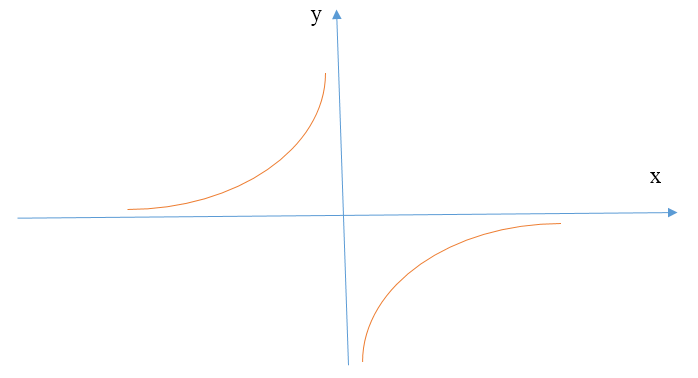
Рисунок 2.

Свойство графика обратной пропорциональности

График симметричен относительно начала координат
График состоит из двух ветвей расположенных если $k > 0$ в I и III координатных четвертях, если $k
График имеет ассимптотами оси координат, т.е ветви гиперболы приближаются к осях $x$ и $y$ , но их не пересекают
График не проходит через начало координат
График не ограничен ни сверху ни снизу
Оласть определения и множества значений функции -- все значения, кроме $0$ , значит, график претерпевает разрыв в точке $(0;0)$