Способы решения систем уравнений
Для начала кратко вспомним, какие вообще существуют способы решения систем уравнений.
Существуют четыре основных способа решения систем уравнений:
Способ подстановки: берется любое из данных уравнений и выражается $y$ через $x$, затем $y$ подставляется в уравнение системы, откуда и находится переменная $x.$ После этого мы легко можем вычислить переменную $y.$
Способ сложения: в данном способе необходимо умножать одно или оба уравнения на такие числа, чтобы при сложении вместе обоих одна из переменных «исчезла».
Графический способ: оба уравнения системы изображается на координатной плоскости и находится точка их пересечения.
Способ введения новых переменных: в этом способе мы делаем замену каких-либо выражений для упрощения системы, а потом применяем один из выше указанных способов.
Системы показательных уравнений
Системы уравнений, состоящие из показательных уравнений, называются системой показательных уравнений.
Решение систем показательных уравнений будем рассматривать на примерах.
Решить систему уравнений
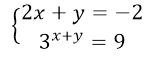
Рисунок 1.
Решение.
Будем пользоваться первым способом для решения данной системы. Для начала выразим в первом уравнении $y$ через $x$.
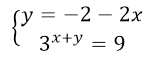
Рисунок 2.
Подставим $y$ во второе уравнение:
\[3^{x-2-2x}=9\] \[3^{-2-x}=3^2\] \[-2-x=2\] \[x=-4\] \[y=-2+8=6\]Ответ: $(-4,6)$.
Решить систему уравнений
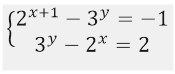
Рисунок 3.
Решение.
Данная система равносильна системе
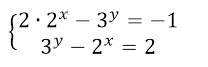
Рисунок 4.
Применим четвертый метод решения уравнений. Пусть $2^x=u\ (u >0)$, а $3^y=v\ (v >0)$, получим:
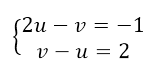
Рисунок 5.
Решим полученную систему методом сложения. Сложим уравнения:
\[2u-v+v-u=-1+2\] \[u=1\]Тогда из второго уравнения, получим, что
\[v=2+u=3\]Возвращаясь к замене, получил новую систему показательных уравнений:
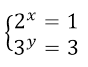
Рисунок 6.
Получаем:
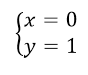
Рисунок 7.
Ответ: $(0,1)$.
Системы показательных неравенств
Cистемы неравенств, состоящие из показательных уравнений, называются системой показательных неравенств.
Решение систем показательных неравенств будем рассматривать на примерах.
Решить систему неравенств
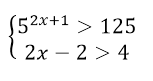
Рисунок 8.
Решение:
Данная система неравенств равносильна системе
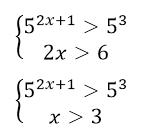
Рисунок 9.
Для решения первого неравенства вспомним следующую теорему равносильности показательных неравенств:
Теорема 1. Неравенство $a^{f(x)} >a^{\varphi (x)} $, где $a >0,a\ne 1$ равносильна совокупности двух систем
\[a^{f(x)} >a^{\varphi (x)} \Leftrightarrow \left[\begin{array}{l} {\left\{\begin{array}{l} {a >1,} \\ {f(x) >\varphi (x);} \end{array}\right. } \\ {\left\{\begin{array}{l} {0Так как в нашем примере $a >1$, то наша система неравенств, по теореме 1, равносильна системе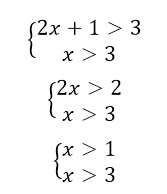
Рисунок 10.
Изобразим оба решения на числовой прямой (рис. 11)
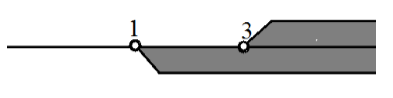
Рисунок 11. Решение примера 3 на числовой прямой
Ответ: $(3,+\infty )$












