Признак подобия прямоугольных треугольников
Введем для начала признак подобия прямоугольных треугольников.
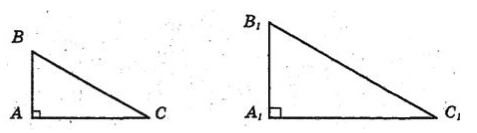
Признак подобия прямоугольных треугольников: два прямоугольных треугольника подобны тогда, когда у них есть по одному равному острому углу (рис. 1).
 прямоугольные треугольники">
прямоугольные треугольники">
Рисунок 1. Подобные прямоугольные треугольники
Доказательство.
Пусть нам дано, что $\angle B=\angle B_1$. Так как треугольники прямоугольные, то $\angle A=\angle A_1={90}^0$. Следовательно, они подобны по первому признаку подобия треугольников.
Теорема доказана.
Теорема о высоте в прямоугольном треугольнике
Высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику.
Доказательство.
Пусть нам дан прямоугольный треугольник $ABC$ с прямым углом $C$. Проведем высоту $CD$ (рис. 2).
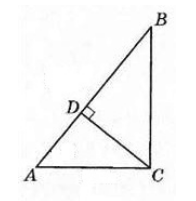
Рисунок 2. Иллюстрация теоремы 2
Докажем, что треугольники $ACD$ и $BCD$ подобны треугольнику $ABC$ и что треугольники $ACD$ и $BCD$ подобны между собой.
-
Так как $\angle ADC={90}^0$, то треугольник $ACD$ прямоугольный. У треугольников $ACD$ и $ABC$ угол $A$ общий, следовательно, по теореме 1, треугольники $ACD$ и $ABC$ подобны.
-
Так как $\angle BDC={90}^0$, то треугольник $BCD$ прямоугольный. У треугольников $BCD$ и $ABC$ угол $B$ общий, следовательно, по теореме 1, треугольники $BCD$ и $ABC$ подобны.
-
Рассмотрим теперь треугольники $ACD$ и $BCD$
\[\angle A={90}^0-\angle ACD\] \[\angle BCD={90}^0-\angle ACD=\angle A\]Следовательно, по теореме 1, треугольники $ACD$ и $BCD$ подобны.
Теорема доказана.
Среднее пропорциональное
Отрезок $x$ называется средним пропорциональным или средним геометрическим дл отрезков $a$ и $b$, если выполняется следующее равенство
\[x=\sqrt{ab}\]Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное для отрезков, на которые высота делит гипотенузу данного треугольника.
Доказательство.
В доказательстве теоремы будем пользоваться обозначениями из рисунка 2.
По теореме 2, имеем, что треугольники $ACD$ и $BCD$ подобны, следовательно
Теорема доказана.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключенным между катетом и высотой, проведенной из вершины угла.
Доказательство.
В доказательстве теоремы будем пользоваться обозначениями из рисунка 2.
По теореме 2, имеем, что треугольники $ACD$ и $ABC$ подобны, следовательно
Теорема доказана.
Примеры задач на использование пропорциональных отрезков в прямоугольном треугольнике
Катеты прямоугольного треугольника $ABC$ с прямым углом $C$ относятся как $2:3$, а гипотенуза равна $39$ см. Найти отрезки, на которые высота $CD$ делит гипотенузу данного треугольника.
Решение.
Изобразим условие на рисунке:
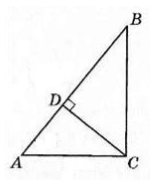
Рисунок 3.
По теореме 4, с одной стороны, получим
\[AC=\sqrt{AB\cdot AD}\]А с другой стороны, получим
\[BC=\sqrt{AB\cdot BD}\]Тогда
\[\frac{AC}{BC}=\frac{\sqrt{AB\cdot AD}}{\sqrt{AB\cdot BD}}=\sqrt{\frac{AD}{BD}}=\frac{2}{3}\]Следовательно
\[\frac{AD}{BD}=\frac{4}{9}\] \[AD=\frac{4}{9}BD\]Так как $AD+BD=AB=39$, то
\[\frac{4}{9}BD+BD=39\] \[13BD=39\cdot 9\] \[BD=27\] \[\ AD=12\]Ответ: $12$ и $27$.











