Пропорциональные отрезки
Для введения понятия подобия вначале нам необходимо вспомнить понятие пропорциональных отрезков. Вспомним также определение отношения двух отрезков.
Отношением двух отрезков называется отношение их длин.
Отрезки $AB$ и $CD$ называются пропорциональными отрезкам $A_1B_1$ и $C_1D_1$, то есть
\[\frac{AB}{CD}=\frac{A_1B_1}{C_1D_1}\]Понятие пропорциональности отрезков имеет место и для большего числа отрезков. Пусть, к примеру, $AB=2$, $CD=4$, $A_1B_1=1$, $C_1D_1=2$, $A_2B_2=4$, $C_2D_2=8$, тогда
То есть отрезки $AB$, $A_1B_1$, $\ A_2B_2$ пропорциональны отрезкам $CD$, $C_1D_1$, $C_2D_2$.
Подобные треугольники
Вспомним для начала, что вообще представляет себе понятие подобия.
Фигуры называются подобными, если они имеет одинаковую форму, но разные размеры.
Разберемся теперь с понятием подобных треугольников. Рассмотрим рисунок 1.
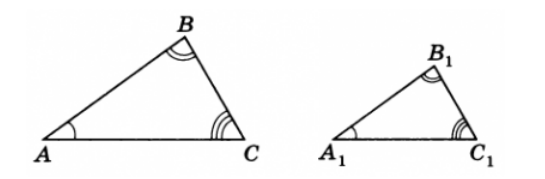
Рисунок 1. Два треугольника
Пусть у этих треугольников $\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1$. Введем следующее определение:
Стороны двух треугольников называются сходственными, если они лежат напротив равных углов этих треугольников.
На рисунке 1, стороны $AB$ и $A_1B_1$, $BC$ и $B_1C_1$, $AC$ и $A_1C_1$ сходственные. Введем теперь определение подобных треугольников.
Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть
\[\angle A=\angle A_1,\ \angle B=\angle B_1,\ \angle C=\angle C_1,\] \[\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}\]На рисунке 1 изображены подобные треугольники.
Обозначение: $ABC\sim A_1B_1C_1$
Для понятия подобия существует также понятие коэффициента подобия.
Число $k$, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.
Площади подобных треугольников
Рассмотрим теперь теорему об отношении площадей подобных треугольников.
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия, то есть
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\]Доказательство.
Рассмотрим два подобных треугольника и обозначим их площади, соответственно $S$ и $S_1$ (рис. 2).
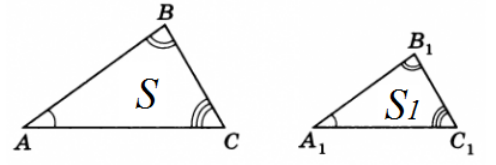
Рисунок 2.
Для доказательства этой теоремы вспомним следующую теорему:
Если угол одного треугольника равен углу второго треугольника, то их площади относятся как произведения сторон, прилегающих к этому углу.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то, по определению,$\angle A=\angle A_1$. Тогда, по теореме 2, получим, что
Так как $\frac{AB}{A_1B_1}=\frac{AC}{A_1C_1}=k$, получим
Теорема доказана.
Задачи, связанные с понятием подобия треугольника
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Стороны первого треугольника $AB=2,\ BC=5,\ AC=6$. Коэффициент подобия данных треугольников $k=2$. Найти стороны второго треугольника.
Решение.
Данная задача имеет два возможных решения.
-
Пусть $k=\frac{A_1B_1}{AB}=\frac{{B_1C}_1}{BC}=\frac{A_1C_1}{AC}$.
Тогда $A_1B_1=kAB,\ {B_1C}_1=kBC,\ A_1C_1=kAC$.
Следовательно, $A_1B_1=4,\ {B_1C}_1=10,\ A_1C_1=12$
-
Пусть $k=\frac{AB}{A_1B_1}=\frac{BC}{{B_1C}_1}=\frac{AC}{A_1C_1}$
Тогда $A_1B_1=\frac{AB}{k},\ {B_1C}_1=\frac{BC}{k},\ A_1C_1=\frac{AC}{k}$.
Следовательно, $A_1B_1=1,\ {B_1C}_1=2,5,\ \ A_1C_1=3$.
Даны подобные треугольники $ABC$ и $A_1B_1C_1.$ Сторона первого треугольника $AB=2$, соответствующая сторона второго треугольника $A_1B_1=6$. Высота первого треугольника $CH=4$. Найти площадь второго треугольника.
Решение.
Так как треугольники $ABC$ и $A_1B_1C_1$ подобны, то $k=\frac{AB}{A_1B_1}=\frac{1}{3}$.
Найдем площадь первого треугольника.
\[S=\frac{1}{2}AB\cdot CH=\frac{1}{2}\cdot 2\cdot 4=4\]По теореме 1, имеем:
\[\frac{S_{ABC}}{S_{A_1B_1C_1}}=k^2\] \[\frac{4}{S_{A_1B_1C_1}}=\frac{1}{9}\] \[S_{A_1B_1C_1}=36\]Ответ: $36$.











