Понятие двугранного угла
Для введения понятия двугранного угла, для начала вспомним одну из аксиом стереометрии.
Любую плоскость можно разделить на две полуплоскости прямой $a$, лежащей в этой плоскости. При этом, точки, лежащие в одной полуплоскости находятся с одной стороны от прямой $a$, а точки, лежащие в разных полуплоскостях -- по разные стороны от прямой $a$ (рис. 1).
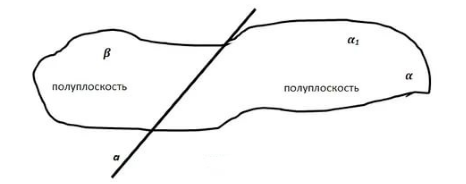
Рисунок 1.
На этой аксиоме основан принцип построение двугранного угла.
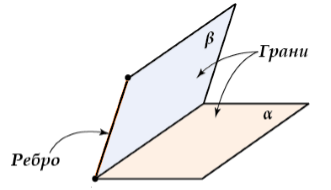
Фигура называется двугранным углом, если она состоит из прямой и двух полуплоскостей этой прямой, не принадлежащих одной плоскости.
При этом полуплоскости двугранного угла называются гранями, а прямая, разделяющая полуплоскости -- ребром двугранного угла (рис. 1).
 Двугранный угол">
Двугранный угол">
Рисунок 2. Двугранный угол
Градусная мера двугранного угла
Выберем на ребре произвольную точку $A$. Угол между двумя прямыми, лежащими в разных полуплоскостях, перпендикулярных ребру и пересекающихся в точке $A$ называется линейным углом двугранного угла (рис. 3).

Рисунок 3.
Очевидно, что каждый двугранный угол имеет бесконечное число линейных углов.
Все линейные углы одного двугранного угла равняются между собой.
Доказательство.
Рассмотрим два линейных угла $AOB$ и $A_1{OB}_1$ (рис. 4).
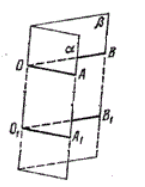
Рисунок 4.
Так как лучи $OA$ и ${OA}_1$ лежат в одной полуплоскости $\alpha $ и перпендикулярны одной прямой, то они являются сонаправленными. Так как лучи $OB$ и ${OB}_1$ лежат в одной полуплоскости $\beta $ и перпендикулярны одной прямой, то они являются сонаправленными. Следовательно
\[\angle AOB=\angle A_1{OB}_1\]В силу произвольности выборов линейных углов. Все линейные углы одного двугранного угла равны между собой.
Теорема доказана.
Градусной мерой двугранного угла называется градусная мера линейного угла двугранного угла.
Примеры задач
Пусть нам даны две неперпендикулярные плоскости $\alpha $ и $\beta $ которые пересекаются по прямой $m$. Точка $A$ принадлежит плоскости $\beta $. $AB$ -- перпендикуляр к прямой $m$. $AC$ перпендикуляр к плоскости $\alpha $ (точка $C$ принадлежит $\alpha $). Доказать, что угол $ABC$ является линейным углом двугранного угла.
Доказательство.
Изобразим рисунок по условию задачи (рис. 5).
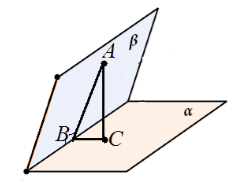
Рисунок 5.
Для доказательства вспомним следующую теорему
Теорема 2: Прямая, проходящая через основание наклонной, перпендикулярно ей, перпендикулярна её проекции.
Так как $AC$ - перпендикуляр к плоскости $\alpha $, то точка $C$ - проекция точки $A$ на плоскость $\alpha $. Следовательно, $BC$ -- проекция наклонной $AB$. По теореме 2, $BC$ перпендикулярна ребру двугранного угла.
Тогда, угол $ABC$ удовлетворяет всем требованиям определения линейного угла двугранного угла.
ч. т. д.
Двугранный угол равен $30^\circ$. На одной из граней лежит точка $A$, которая удалена от другой грани на расстояние $4$ см. Найти расстояние от точки $A$ до ребра двугранного угла.
Решение.
Будем рассматривать рисунок 5.
По условию, имеем $AC=4\ см$.
По определению градусной меры двугранного угла, имеем, что угол $ABC$ равен $30^\circ$.
Треугольник $ABC$ является прямоугольным треугольником. По определению синуса острого угла
\[\frac{AC}{AB}=sin{30}^0\] \[\frac{5}{AB}=\frac{1}{2}\] \[AB=10\]Ответ: $10$ см.













