Шар
Шар является геометрическим пространственным телом.
Вокруг нас очень много предметов, которые имеют форму шара: арбуз, горох, апельсин, стальной шарик и т.п. Форму шара имеет и планета Земля.
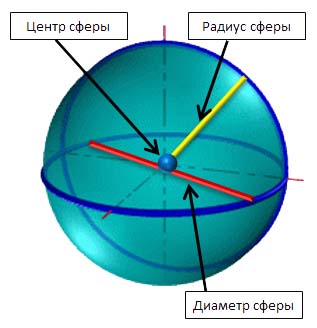
Шар имеет центр и характеризуется длиной радиуса и диаметра.
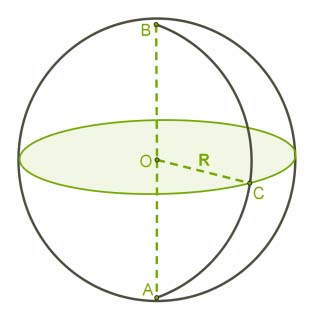
На рисунке изображен шар, который имеет центр в точке $O$. Все точки на поверхности шара расположены на одинаковом расстоянии от центра шара. Это значит, что если выбрать на поверхности любые точки, например, точки $A, B \ и \ C,$ соединить их с центром шара, то получим отрезки, которые будут равны между собой:
$OA=OB=OC.$
Отрезок, который соединяет любую точку поверхности шара с его центром, называется радиусом шара.
Следовательно, $OA, OB \ и \ OC$ – радиусы шара.
Очевидно, что центр шара можно соединить с бесконечным числом точек на поверхности шара. Из этого следует, что можно провести бесконечное множество радиусов шара.
На рисунке изображен отрезок $AB$, который проходит через центр шара и соединяет $2$ точки поверхности шара.
Отрезок $AB$ является диаметром шара. Причем отрезок $AB$ состоит из двух равных отрезков $OA$ и $OB$, которые являются радиусами шара.
Таким образом, длина диаметра шара равна двум его радиусам.
Диаметр шара – отрезок, который соединяет две точки поверхности шара и проходит через его центр.
Объем шара
Шар внутри не пустотелый, а заполненный, к тому же, с точки зрения математики является пространственным телом. Таким образом, можно найти его объем.
Объем шара вычисляется по следующей формуле:
$V=\frac{4}{3} πR^3$.
Используя определение степени, формула объема шара может быть записана в следующем виде:
$V=\frac{4}{3} πR^3=\frac{4}{3} πR \cdot R \cdot R$.
Найти объем шара, если его радиус равен $5 \frac{3}{7}$ см.
Решение.
Воспользуемся формулой объема шара и подставим в нее значение радиуса и числа Пи:
$V=\frac{4}{3} πR^3=\frac{4}{3} \cdot 3,14 \cdot (5 \frac{3}{7})^3=\frac{4}{3} \cdot 3,14 \cdot (\frac{38}{7})^3=\frac{4 \cdot 3,14}{3} \cdot \frac{54872}{343}=\frac{689192,32}{1029}≈669,77 \ см^3$
Ответ: $V≈669,77 \ см^3$.
Вычислить радиус шара, если его объем равен $3 \frac{16}{27} \ см^3$.
Решение.
Воспользуемся формулой объема шара и выразим из нее радиус шара:
$V=\frac{4}{3} πR^3$;
$\frac{4}{3} πR^3=V$;
$πR^3=\frac{3}{4} V$;
$R^3=\frac{3V}{4π}$.
Подставим известное значение объема в полученную формулу:
$R^3=\frac{3V}{4π}=\frac{3 \cdot 3 \frac{16}{27}}{4 \cdot 3,14}=\frac{3 \cdot 3 \frac{16}{27}}{4 \cdot 3,14}=\frac{3 \cdot \frac{97}{27}}{12,56}=\frac{97}{9 \cdot 12,56}=\frac{97}{113,04}≈0,8581$
$R≈0,95 см$.
Ответ: $R≈0,95 см$.
Сфера
Древние мыслители и ученые с помощью сферической формы, совершенство которой издавна привлекало их внимание, пытались объяснить гармонию окружающего мира. Например, древние греки представляли вращающуюся хрустальную сферу, к которой были прикреплены звёзды. Древнегреческие ученые создавали космологические модели Земли, которые имели сферическую форму и к которым были прикреплены вращающиеся сферы – планеты.
Поверхность шара называется сферой.
Примерами сферы можно назвать волейбольный мяч, теннисный мяч.
Невозможно развернуть сферу на плоскости. Например, на географических картах видно, что полярные области растянуты, изображены с искажением.
Сфера, как и шар, имеет центр, радиус и диаметр.
Для сферы можно вычислить площадь ее поверхности.
Площадь сферы
Площадь сферы вычисляется по формуле:
$S = 4πR^2$.
Для вычисления площади сферы нужно ознакомиться с понятием степени числа, зная определение которой формулу площади сферы можно переписать в следующем виде:
$S = 4πR^2= 4πR \cdot R$.
Вычислить площадь сферы, если её радиус равен $2 \frac{4}{5}$ см.
Решение.
Воспользуемся формулой площади сферы:
$S = 4πR^2$.
Подставим значение радиуса в формулу и, используя преобразование дробей и правила умножения дробей, найдем результат:
$S=4πR^2=4 \cdot 3,14 \cdot (2 \frac{4}{5})^2=4 \cdot 3,14 \cdot (\frac{14}{5})^2=4 \cdot 3,14 \cdot \frac{196}{25}=\frac{4 \cdot 3,14 \cdot 196}{25}=\frac{2461,76}{25}≈98,47 \ см^2$.
Ответ: $S≈98,47 \ см^2$.