
Пусть $X$ -- непрерывная случайная величина.
Случайная величина $X$ имеет нормальное распределение (распределение Гаусса), если плотность её распределения определяется формулой:
\[\varphi \left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{(x-a)}^2}{2{\sigma }^2}}\]Здесь $aϵR$ -- математическое ожидание, а $\sigma >0$ -- среднее квадратическое отклонение.
Плотность нормального распределения.
Покажем, что эта функция действительно является плотностью распределения. Для этого проверим следующее условие:
Рассмотрим несобственный интеграл $\int\limits^{+\infty }_{-\infty }{\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{(x-a)}^2}{2{\sigma }^2}}dx}$.
Сделаем замену: $\frac{x-a}{\sigma }=t,\ x=\sigma t+a,\ dx=\sigma dt$.
Так как $f\left(t\right)=e^{\frac{-t^2}{2}}$ четная функция, то
Равенство выполняется, значит, функция $\varphi \left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{(x-a)}^2}{2{\sigma }^2}}$ действительно является плотностью распределения некоторой случайной величины.
Рассмотрим некоторые простейшие свойства функции плотности вероятности нормального распределения $\varphi \left(x\right)$:
- График функции плотности вероятности нормального распределения симметричен относительно прямой $x=a$.
- Функция $\varphi \left(x\right)$ достигает максимума при $x=a$, при этом $\varphi \left(a\right)=\frac{1}{\sqrt{2\pi }\sigma }e^{\frac{-{(a-a)}^2}{2{\sigma }^2}}=\frac{1}{\sqrt{2\pi }\sigma }$
- Функция $\varphi \left(x\right)$ убывает, при $x>a$, и возрастает, при $x
- Функция $\varphi \left(x\right)$ имеет точки перегиба при $x=a+\sigma $ и $x=a-\sigma $.
- Функция $\varphi \left(x\right)$ асимптотически приближается к оси $Ox$ при $x\to \pm \infty $.
- Схематический график выглядит следующим образом (рис. 1).
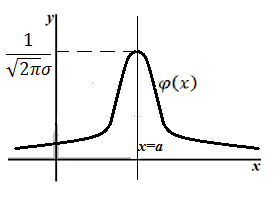
Рисунок 1. Рис. 1. График плотности нормального распределения
!!! Заметим, что, если $a=0$, то график функции симметричен относительно оси $Oy$. Следовательно, функция $\varphi \left(x\right)$ четна.
Функция нормального распределения вероятности.
Для нахождения функции распределения вероятности при нормальном распределении воспользуемся следующей формулой:
Следовательно,
Функция $F(x)$ называется стандартным нормальным распределением, если $a=0,\ \sigma =1$, то есть:
\[F\left(x\right)=\frac{1}{\sqrt{2\pi }}\int\limits^x_{-\infty }{e^{\frac{-t^2}{2}}dt}=\frac{1}{\sqrt{2\pi }}\left(\int\limits^0_{-\infty }{e^{\frac{-t^2}{2}}dt}+\int\limits^x_0{e^{\frac{-t^2}{2}}dt}\right)=0,5+Ф(x)\]Здесь $Ф\left(x\right)=\frac{1}{\sqrt{2\pi }}\int\limits^x_0{e^{\frac{-t^2}{2}}dt}$ - функция Лапласса.
Функция $Ф\left(x\right)=\frac{1}{\sqrt{2\pi }}\int\limits^x_0{e^{\frac{-t^2}{2}}dt}$ называется интегралом вероятности.
Числовые характеристики нормального распределения.
Математическое ожидание: $M\left(X\right)=a$.
Дисперсия: $D\left(X\right)={\sigma }^2$.
Среднее квадратическое распределение: $\sigma \left(X\right)=\sigma $.
Пример решения задачи на понятие нормального распределения.
Задача 1: Длина пути $X$ представляет собой случайную непрерывную величину. $X$ распределена по нормальному закону распределения среднее значение которого равно $4$ километра, а среднее квадратическое отклонение равно $100$ метров.
- Найти функцию плотности распределения $X$.
- Построить схематически график плотности распределения.
- Найти функцию распределения случайной величины $X$.
- Найти дисперсию.
Решение:
- Для начала представим все величины в одном измерении: 100м=0,1км
Из определения 1, получим:
\[\varphi \left(x\right)=\frac{1}{0,1\sqrt{2\pi }}e^{\frac{-{(x-4)}^2}{0,02}}\](так как $a=4\ км,\ \sigma =0,1\ км)$
- Используя свойства функции плотности распределения, имеем, что график функции $\varphi \left(x\right)$ симметричен относительно прямой $x=4$.
Максимум функция достигает в точке $\left(a,\frac{1}{\sqrt{2\pi }\sigma }\right)=(4,\ \frac{1}{0,1\sqrt{2\pi }})$
Схематический график имеет вид:
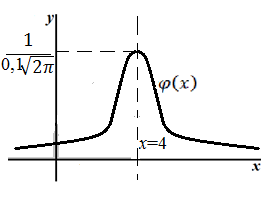
Рисунок 2.
- По определению функции распределения $F\left(x\right)=\frac{1}{\sqrt{2\pi }\sigma }\int\limits^x_{-\infty }{e^{\frac{-{(t-a)}^2}{2{\sigma }^2}}dt}$, имеем:
- $D\left(X\right)={\sigma }^2=0,01$.











