Понятие призмы
Геометрическая фигура, образованная двумя равными $n-$угольниками, лежащими в параллельных плоскостях, вершины которых соединены между собой так, что соответствующая вершина первого $n-$угольника соединена с соответствующей вершиной второго $n-$уголника, называется призмой (рис. 1).
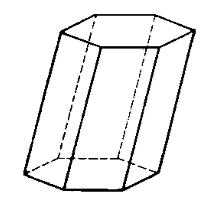
Рисунок 1. Призма
Параллельные $n-$уголники называются основаниями призмы, параллелограммы их соединяющие -- боковыми гранями, стороны параллелограммов -- сторонами призмы, а вершины $n-$угольников -- вершинами призмы.
Виды призм
В зависимости от количества углов в основании призмы ее можно назвать треугольной, четырехугольной и так далее (рис. 2).
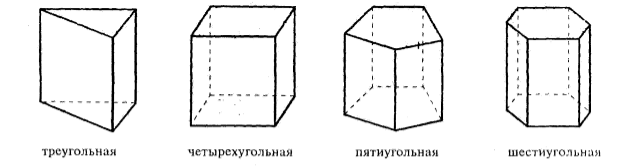
Рисунок 2.
Отметим, что параллелепипед является частным случаем четырехугольной призмы.
Призма, у которой все двугранные углы равны ${90}^0$ называется прямой (рис. 3). В противном же случае она является наклонной.
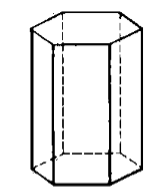
Рисунок 3. Прямая призма
Прямая призма, в основании которой лежат правильные $n-$уголники называется правильной (рис. 4).
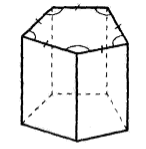
Рисунок 4.
Площадь призмы
Полная площадь призмы определяется следующим образом
где $S_{бок}$ - сумма площадей всех ее боковых граней, а $S_{осн}$ - площадь основания данной призмы.
Рассмотрим и докажем следующую теорему.
Площадь боковой поверхности прямой призмы определяется как произведение периметра основания данной призмы на ее высоту.
Доказательство.
Рассмотрим прямую $n-$угнольную призму, длины оснований которой равны $a_1,\ a_2,\dots ,a_n$ соответственно. Как мы знаем, высота прямой призмы равняется боковой стороне данной призмы. Обозначим её через $h$. Тогда, так как боковые грани являются прямоугольниками, площади боковых граней равняются, соответственно
Так как площадь боковой поверхности -- сумма площадей всех боковых граней, то
Теорема доказана.
Объем призмы
Объем прямой призмы с прямым треугольником при основании определяется как произведение площади его основания на высоту.
Доказательство.
Рассмотрим прямую призму $ABDA_1B_1D_1$ c прямоугольным треугольником при основании. Дополним его до прямоугольного параллелепипеда (рис. 5)
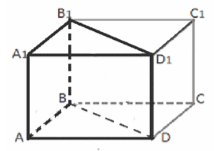
Рисунок 5.
Следовательно,
Теорема доказана.
Объем прямой призмы определяется как произведение площади его основания на высоту.
Доказательство.
-
Рассмотрим прямую треугольную призму $ABDA_1B_1D_1$. Разделим ее на две призмы с прямыми треугольниками при основании с объемами $V_1\ и\ V_2$ ($BC$ и $B_1C_1$ -- высоты оснований) (рис. 6).
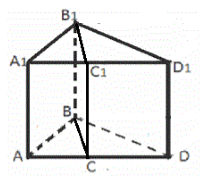
Рисунок 6.По теореме 2, получим
\[V_{пр}=V_1+\ V_2=S_{ABC}h+S_{DBC}h={h(S}_{ABC}+S_{DBC})=S_{осн}h\] -
Любую призму мы всегда может разделять на несколько прямоугольных призм, следовательно эта формула верна для произвольно размерной прямой призмы.
Теорема доказана.
Пример задачи
Найти объем прямой призмы с равнобедренным треугольником при основании и высотой $h=3$, если боковая сторона треугольника равна $4$, а угол между ними равен ${30}^0$.
Решение.
Так как боковая сторона основания равна $3$, а угол между ними равен ${30}^0$. То
\[S_{осн}=\frac{1}{2}\cdot 4\cdot 4\cdot sin{30}^0=8\cdot \frac{1}{2}=4\]По теореме 3, получим
\[V=4\cdot 3=12\]Ответ: $12.$












