Начальные сведения об углах
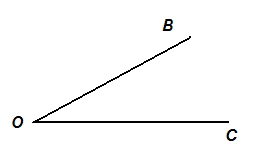
Пусть нам даны два произвольных луча. Наложим их начала друг на друга. Тогда
Углом будем называть два луча, которые имеют одно и тоже начало.
Точка, которая является началом лучей в рамках определения 3, называется вершиной этого угла.
Угол будем обозначать следующими тремя её точками: вершиной, точкой на одном из лучей и точкой на другом луче, причем вершина угла записывается в середине его обозначения (рис. 1).
Определим теперь, что такое величина угла.
Для этого необходимо выбрать какой-то «эталонный» угол, который мы будем принимать за единицу. Чаще всего таким углом является угол, который равен $\frac{1}{180}$ части развернутого угла. Такую величину называют градусом. После выбора такого угла мы проводим с ним сравнение углов, величину которого нужно найти.
Существуют 4 вида углов:
Угол называется острым, если он меньше $90^0$.
Угол называется тупым, если он больше $90^0$.
Угол называется развернутым, если он равен $180^0$.
Угол называется прямым, если он равен $90^0$.
Помимо таких видов углов, которые описаны выше, можно выделять виды углов по отношению их друг к другу, а именно вертикальные и смежные углы.
Смежные углы
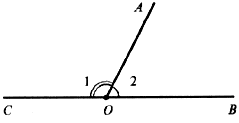
Рассмотрим развернутый угол $COB$. Из его вершины проведем луч $OA$. Этот луч разделит первоначальный на два угла. Тогда
Два угла будем называть смежными, если одна пара их сторон является развернутым углом, а другая пара совпадает (рис. 2).
В данном случае углы $COA$ и $BOA$ являются смежными.
Сумма смежных углов равняется $180^0$.
Доказательство.
Рассмотрим рисунок 2.
По определению 7, в нем угол $COB$ будет равняться $180^0$. Так как вторая пара сторон смежных углов совпадает, то луч $OA$ будет разделять развернутый угол на 2, следовательно
$∠COA+∠BOA=180^0$
Теорема доказана.
Рассмотрим решение задачи с помощью данного понятия.
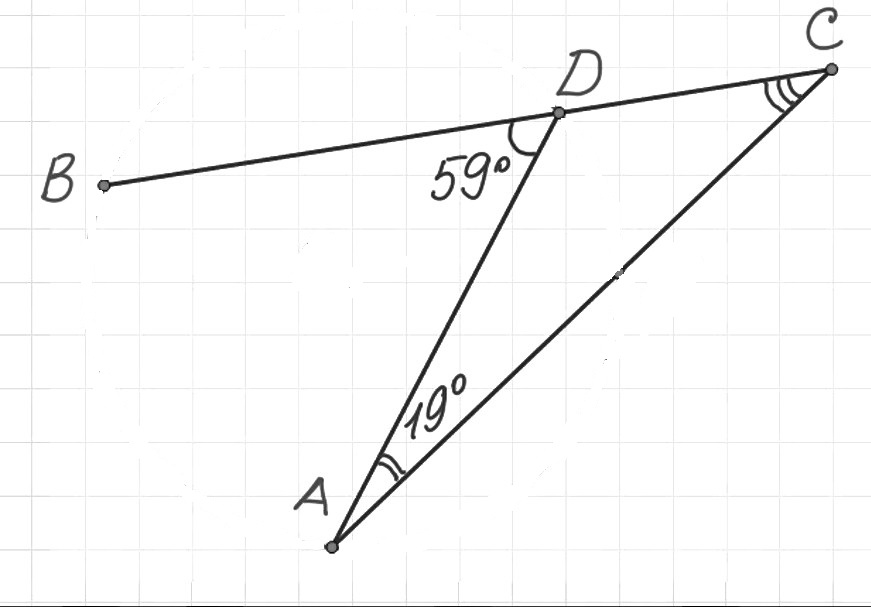
Найти угол $C$ из рисунка ниже
Решение.
По определению 7 получаем, что углы $BDA$ и $ADC$ являются смежными. Следовательно, по теореме 1, получим
$∠BDA+∠ADC=180^0$
$∠ADC=180^0-∠BDA=180〗0-59^0=121^0$
По теореме о сумме углов в треугольнике, будем иметь
$∠A+∠ADC+∠C=180^0$
$∠C=180^0-∠A-∠ADC=180^0-19^0-121^0=40^0$
Ответ: $40^0$.
Вертикальные углы
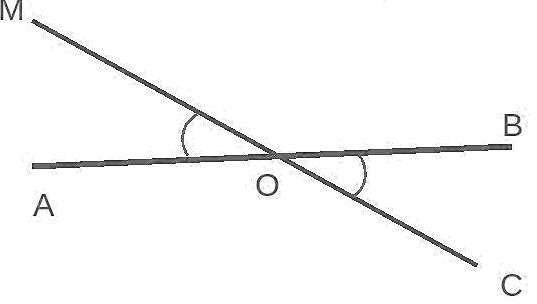
Рассмотрим развернутые углы $AOB$ и $MOC$. Совместим их вершины между собой (то есть наложим точку $O'$ на точку $O$) так, чтобы никакие стороны этих углов не совпали. Тогда
Два угла будем называть вертикальными, если пары их сторон являются развернутыми углами, а их величины совпадают (рис. 3).
В данном случае углы $MOA$ и $BOC$ являются вертикальными и углы $MOB$ и $AOC$ также вертикальные.
Вертикальные углы равняются между собой.
Доказательство.
Рассмотрим рисунок 3. Докажем, к примеру, что угол $MOA$ равняется углу $BOC$.
По определению 7, видим, что углы $AOM$ и $MOB$, а также углы $COB$ и $MOB$ будет являться смежными. Обозначим угол $MOB$ через $β$. По теореме 1, получим
$∠AOM+β=180^0$
$∠AOM=180^0-β$
С другой стороны
$∠COB+β=180^0$
$∠COB=180^0-β$
Получаем, что
$∠AOM=∠COB$
Теорема доказана.
Рассмотрим решение задачи с помощью данного понятия.
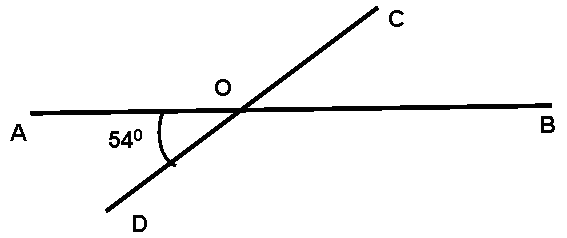
Найти угол $COB$ из рисунка ниже
Решение.
По определению 8 получаем, что углы $AOD$ и $COB$ являются вертикальными. Следовательно, по теореме 2, получим
$∠COB=∠AOD=54^0$
Ответ: $54^0$.
Пример смешанной задачи
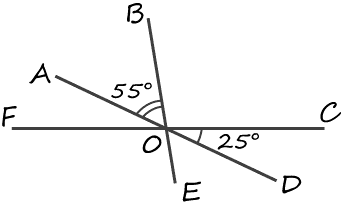
Найти угол $COB$ из рисунка ниже
Решение. По определению 8 получаем, что углы $FAO$ и $COD$ являются вертикальными. Следовательно, по теореме 2, получим
$∠FAO=∠COD=25^0$
По определению 7 получаем, что углы $BOF$ и $BOC$ являются смежными. Следовательно, по теореме 1, получим
$∠BOF+∠BOC=180^0$
$∠BOC=180^0-∠BOF=180^0-55^0-25^0=100^0$
Ответ: $100^0$.