Предварительные сведения о прямых
Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.
Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины. Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Сама же прямая является бесконечной на обоих своих концах.
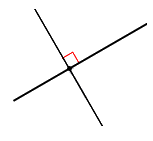
Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках (рис. 1).
Понятия прямой и точки связаны тремя аксиомами геометрии:
Аксиома 1: Для каждой произвольной прямой существует как минимум две точки, которые на ней лежат.
Аксиома 2: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Аксиома 3: Через 2 произвольные точки всегда проходит прямая, причем эта прямая единственна.
Для двух прямых актуально их взаимное расположение. Возможны три случая:
- Две прямые совпадают. В этом случае каждая точка одной будет также и точкой другой прямой.
- Две прямые пересекаются. В этом случае только какая-то одна точка из одной прямой будет также принадлежать и другой прямой.
- Две прямые параллельны. В этом случае у каждой из этих прямых свой набор различных друг от друга точек.
Перпендикулярность прямых
Рассмотрим две произвольные пересекающиеся прямые. Очевидно, что в точке их пересечения образовывается 4 угла. Тогда
Пересекающиеся прямые будем называть перпендикулярными, если хотя бы один угол, образованный их пересечением равняется $90^0$ (рис. 2).
Обозначение: $a⊥b$.
Рассмотрим следующую задачу:
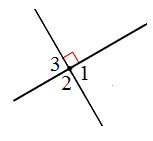
Найти углы 1, 2 и 3 из рисунка ниже
Решение.
Угол 2 является вертикальным для данного нам угла, следовательно
$∠2=90^0$
Угол 1 является смежным для угла 2, следовательно
$∠1=180^0-∠2=180^0-90^0=90^0$
Угол 3 является вертикальным для угла 1, следовательно
$∠3=∠1=90^0$
Из этой задачи можем сделать следующее замечание
Все углы между перпендикулярными прямыми равняются $90^0$.
Основная теорема перпендикулярных прямых
Введем следующую теорему:
Две прямые, являющиеся перпендикулярными для третьей будут непересекающимися.
Доказательство.
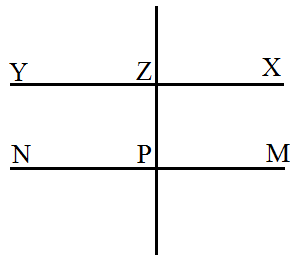
Рассмотрим рисунок 3 по условию задачи.
Разделим мысленно данный рисунок на две части прямой $(ZP)$. Наложим правую часть на левую. Тогда, так как прямые $(NM)$ и $(XY)$ перпендикулярны к прямой $(PZ)$ и, следовательно, углы между ними прямые, то луч $NP$ наложется целиком на луч $PM$, а луч $XZ$ наложется целиком на луч $YZ$.
Теперь, предположим противное: пусть эти прямые пересекаются. Без ограничения общности предположим, что они пересекаются с левой стороны, то есть, пусть луч $NP$ пересекается с лучом $YZ$ в точке $O$. Тогда, по конструкции, описанной выше, будем получать, что и луч $PM$ пересекается с лучом $YZ$ в точке $O'$. Но тогда мы получаем, что через две точки $O$ и $O'$, проходит две прямые $(NM)$ и $(XY)$, что противоречит аксиоме 3 прямых.
Следовательно, прямые $(NM)$ и $(XY)$ не пересекаются.
Теорема доказана.
Пример задачи
Даны две прямые, которые имеют точку пересечения. Через точку, которая не принадлежит ни одной из них проведены две прямые, одна из которых перпендикулярна одной из выше описанных прямых, а другая - другой из них. Доказать, что они не совпадают.
Решение.
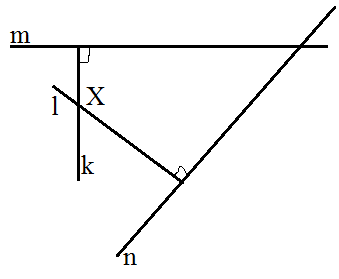
Изобразим рисунок по условию задачи (рис. 4).
Из условия задачи будем иметь, что $m⊥k,n⊥l$.
Предположим противное, пусть прямые $k$ и $l$ совпадают. Пусть это будет прямой $l$. Тогда, по условию $m⊥l$ и $n⊥l$. Следовательно, по теореме 1, прямые $m$ и $n$ не пересекаются. Получили противоречие, а значит прямые $k$ и $l$ не совпадают.