Предварительные сведения
Здесь мы ограничимся двумерным случаем. Введение понятия для трехмерного случая проводится аналогично. Для того, чтобы ввести понятие координат вектора сначала введем и докажем следующие лемму и теорему.
Лемма 1: Если векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ коллинеарны, и вектор $\overrightarrow{a}$ не является нулевым, то существует действительное число $k$, такое что выполняется равенство$\overrightarrow{b}=k\overrightarrow{a}$
Доказательство.
Возможны два случая:
-
$\overrightarrow{a}\uparrow \uparrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены, а $k\ge 0$, то векторы $k\overrightarrow{a}$ и $\overrightarrow{b}$ сонаправлены. Далее, имеем, что
\[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
-
$\overrightarrow{a}\uparrow \downarrow \overrightarrow{b}$
Обозначим число $k$ следующим образом: $k=-\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}$. Так как векторы $\overrightarrow{a}$ и $\overrightarrow{b}$ противоположно направленные, а $k \[\left|k\overrightarrow{a}\right|=\left|k\right|\left|\overrightarrow{a}\right|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}\left|\overrightarrow{a}\right|=|\overrightarrow{b}|\]
Из этого всего следует, что $\overrightarrow{b}=k\overrightarrow{a}$.
Лемма доказана.
Любой вектор можно разложить по двум неколлинеарным векторам, причем коэффициенты разложения определяются единственным образом:
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]Доказательство.
Существование: Докажем, что такое разложение имеет место. Здесь возможны два случая:
-
Вектор $\overrightarrow{c}$ коллинеарен (к примеру) вектору $\overrightarrow{b}$.
По лемме 1, будем иметь
\[\overrightarrow{c}=n\overrightarrow{b}\]Значит, если число $m=0$, то получим
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\] -
Вектор $\overrightarrow{c}$ не коллинеарен векторам $\overrightarrow{a}$ и $\overrightarrow{b}$.
Возьмем произвольную точку $O$ и отложим от нее векторы $\overrightarrow{OB}=\overrightarrow{b},\ \overrightarrow{OA}=\overrightarrow{a}$ и $\overrightarrow{OC}=\overrightarrow{c}$. Пусть Проведем прямую $CD||OB$ (рис. 1)
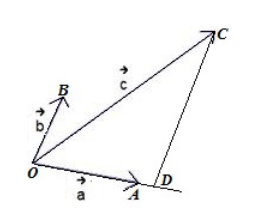
Рисунок 1. Иллюстрация теоремы 1По правилу треугольника для сложения векторов, получим
\[\overrightarrow{c}=\overrightarrow{OD}+\overrightarrow{DC}\]По построению, получаем что векторы $\overrightarrow{OD}||\overrightarrow{a}$ и $\overrightarrow{DC}||\overrightarrow{b}$, следовательно, по лемме 1, имеем
\[\overrightarrow{OD}=m\overrightarrow{a},\ \overrightarrow{DC}=n\overrightarrow{b}\]Значит
\[\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}\]
Единственность: Предположим противное, что помимо разложения$\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}$ существует разложение $\overrightarrow{c}=m'\overrightarrow{a}+n'\overrightarrow{b}$. Вычтем эти два равенства из друг друга:
Получаем систему:
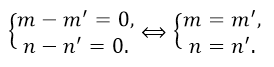
Рисунок 2.
Следовательно, разложение единственно.
Теорема доказана.
Координаты вектора
Рассмотрим далее систему координат. От начала координат $O$ в направлении оси $Ox$ отложим вектор $\overrightarrow{i}$, а в направлении оси $Oy$ отложим вектор $\overrightarrow{j}$, длины которых равны единице.
Векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ называются координатными векторами.
Так как векторы $\overrightarrow{i}$ и $\overrightarrow{j}$ не коллинеарны то, по теореме 1, любой вектор можно разложить в виде $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$.
Коэффициенты разложения вектора $\overrightarrow{c}=m\overrightarrow{i}+n\overrightarrow{j}$ называются координатами данного вектора в данной системе координат, то есть
\[\overrightarrow{c}=\{m,\ n\}\]Линейные операции над векторами
Теорема о сумме векторов: Координаты суммы векторов равны сумме соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Теорема о разности векторов: Координаты разности векторов равны разности соответствующих координат этих векторов.
Доказательство.
Докажем теорему для двух векторов. Теорема для большего количества векторов доказывается аналогично. Пусть $\overrightarrow{a}=\left\{x_1,\ y_1\right\}$, $\overrightarrow{b}=\{x_2,\ y_2\}$, тогда
Следовательно
Теорема доказана.
Доказательство.
Пусть $\overrightarrow{a}=\left\{x,\ y\right\}$, тогда $\overrightarrow{a}=x\overrightarrow{i}+\ y\overrightarrow{j}.$
Следовательно
Теорема доказана.
Пример задачи на нахождение координат вектора
Пусть $\overrightarrow{a}=\left\{3,\ 4\right\}$, $\overrightarrow{b}=\{2,\ -1\}$. Найти $\overrightarrow{a}+\overrightarrow{b}$, $\overrightarrow{a}-\overrightarrow{b}$ и $3\overrightarrow{a}$.
Решение.
\[\overrightarrow{a}+\overrightarrow{b}=\left\{3+2,\ 4-1\right\}=\{5,\ 3\}\] \[\overrightarrow{a}-\overrightarrow{b}=\left\{3-2,\ 4+1\right\}=\{1,\ 5\}\] \[3\overrightarrow{a}=\left\{3\cdot 3,3\cdot 4\right\}=\{9,12\}\]











