Определение функции распределения
Пусть $X$ – случайная величина, а $x$ – вероятность распределения этой случайной величины.
Функцией распределения называется функция $F(x)$ удовлетворяющая условию $F\left(x\right)=P(X
Также иначе функцию распределения иногда называются интегральной функцией распределения или интегральным законом распределения.
В общем виде график функции распределения представляет собой график неубывающей функции с областью значений, принадлежащей отрезку $\left[0,1\right]$ (причем 0 и 1 обязательно входят в область значений). При этом функция может, как иметь, так и не иметь скачков функции (рис. 1)
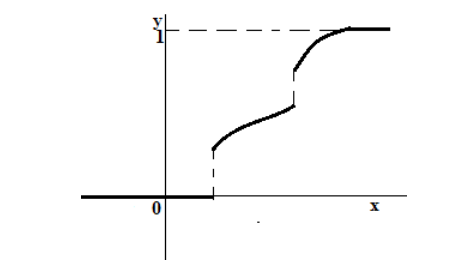
Рисунок 1. Пример графика функции распределения
Функция распределения дискретной случайной величины
Пусть случайная величина $X$ является дискретной. И пусть для нее дан ряд её распределения. Для такой величины функцию распределения вероятностей можно записать в следующем виде:
ступенчатую функцию
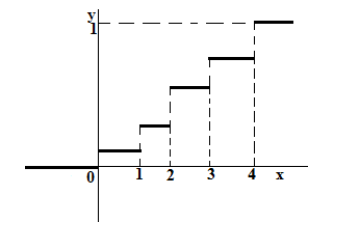
Функция распределения непрерывной случайной величины
Пусть случайная величина $X$ теперь является непрерывной.
График функции распределения такой случайной величины всегда представляет собой неубывающую непрерывную функцию (рис. 3).
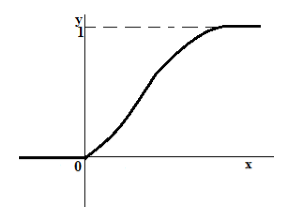
Функция распределения смешанной случайной величины
Рассмотрим теперь случай, где случайная величина $X$ является смешанной.
График функции распределения такой случайной величины всегда представляет собой неубывающую функцию, которая имеет минимальное значение в 0, максимальное значение в 1, но которая не на всей области определения является непрерывной функцией (то есть имеет скачки в отдельных точках) (рис. 4).
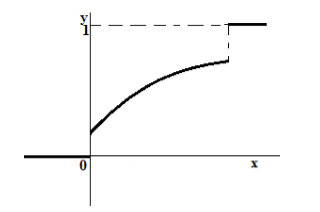
Рисунок 4. Функция распределения смешанной случайной величины
Примеры задач на нахождение функции распределения
Приведен ряд распределений появления события $A$ в трех опытах

Рисунок 5.
Найти функцию распределения вероятностей и построить её график.
Решение.
Так как случайная величина является дискретной, то мы можем пользоваться формулой $\ F\left(x\right)=\sum\limits_{x_i
При $x\le 0$, $F\left(x\right)=0$;
При $0
При $1
При $2
При $x>3$, $F\left(x\right)=0,2+0,1+0,3+0,4=1$;
Отсюда получаем следующую функцию распределения вероятностей:
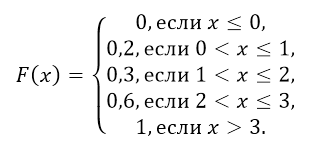
Рисунок 6.
Построим ее график:
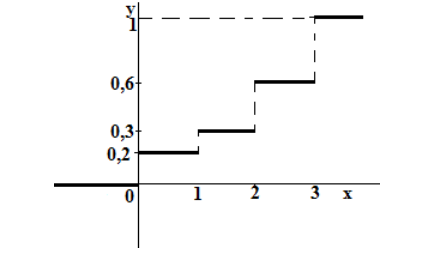
Рисунок 7.
Проводится один опыт, в котором событие $A$ может, как произойти, так и не произойти. Вероятность того, что данное событие произойдет равно $0,6$. Найти и построить функцию распределения случайной величины.
Решение.
Так как вероятность того, что событие $A$ произойдет равно $0,6$, то вероятность того, что данное событие не произойдет равно $1-0,6=0,4$.
Построим для начала ряд распределения данной случайной величины:

Рисунок 8.
Так как случайная величина является дискретной, найдем функцию распределения по аналогии с задачей 1:
При $x\le 0$, $F\left(x\right)=0$;
При $0
При $x>1$, $F\left(x\right)=0,4+0,6=1$;
Таким образом, получаем следующую функцию распределения:
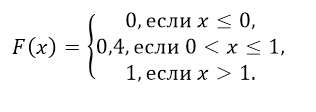
Рисунок 9.
Построим ее график:
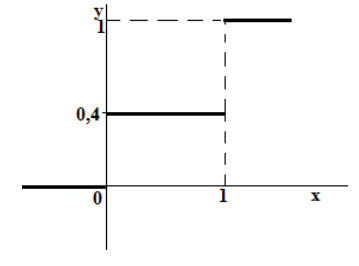
Рисунок 10.












