Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
В отношении функции $z=f(x,y)$ рассмотрим понятия общего (полного) и частного приращений функции.
Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.
Так как переменные $(x,y)$ являются независимыми, то одна из них может изменяться, а другая при этом сохранять постоянное значение.
Дадим переменной $x$ приращение $\Delta x$, при этом сохраним значение переменной $y$ неизменным.
Тогда функция $z=f(x,y)$ получит приращение, которое будет называться частным приращением функции $z=f(x,y)$ по переменной $x$. Обозначение:
Аналогично дадим переменной $y$ приращение $\Delta y$, при этом сохраним значение переменной $x$ неизменным.
Тогда функция $z=f(x,y)$ получит приращение, которое будет называться частным приращением функции $z=f(x,y)$ по переменной $y$. Обозначение:
Если же аргументу $x$ дать приращение $\Delta x$, а аргументу $y$ - приращение $\Delta y$, то получается полное приращение заданной функции $z=f(x,y)$. Обозначение:
Таким образом, имеем:
-
$\Delta _{x} z=f(x+\Delta x,y)-f(x,y)$ - частное приращение функции $z=f(x,y)$ по $x$;
-
$\Delta _{y} z=f(x,y+\Delta y)-f(x,y)$ - частное приращение функции $z=f(x,y)$ по $y$;
-
$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$ - полное приращение функции $z=f(x,y)$.
Записать частные и полное приращение функции
\[z=x+y.\]Решение:
По определению частного приращения найдем:
$\Delta _{x} z=x+\Delta x+y$ - частное приращение функции $z=f(x,y)$ по $x$;
$\Delta _{y} z=x+y+\Delta y$ - частное приращение функции $z=f(x,y)$ по $y$.
По определению полного приращения найдем:
$\Delta z=x+\Delta x+y+\Delta y$ - полное приращение функции $z=f(x,y)$.
Вычислить частные и полное приращение функции $z=xy$ в точке $(1;2)$ при $\Delta x=0,1;\, \, \Delta y=0,1$.
Решение:
По определению частного приращения найдем:
$\Delta _{x} z=(x+\Delta x)\cdot y$ - частное приращение функции $z=f(x,y)$ по $x$
$\Delta _{y} z=x\cdot (y+\Delta y)$ - частное приращение функции $z=f(x,y)$ по $y$;
По определению полного приращения найдем:
$\Delta z=(x+\Delta x)\cdot (y+\Delta y)$ - полное приращение функции $z=f(x,y)$.
Следовательно,
\[\Delta _{x} z=(1+0,1)\cdot 2=2,2\] \[\Delta _{y} z=1\cdot (2+0,1)=2,1\] \[\Delta z=(1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]Полное приращение заданной функции $z=f(x,y)$ не равно сумме ее частных приращений $\Delta _{x} z$ и $\Delta _{y} z$. Математическая запись: $\Delta z\ne \Delta _{x} z+\Delta _{y} z$.
Проверить утверждение замечания для функции
\[z=x+y.\]Решение:
$\Delta _{x} z=x+\Delta x+y$; $\Delta _{y} z=x+y+\Delta y$; $\Delta z=x+\Delta x+y+\Delta y$ (получены в примере 1)
Найдем сумму частных приращений заданной функции $z=f(x,y)$
\[\Delta _{x} z+\Delta _{y} z=x+\Delta x+y+(x+y+\Delta y)=2\cdot (x+y)+\Delta x+\Delta y.\]Так как
\[2\cdot (x+y)+\Delta x+\Delta y\ne x+\Delta x+y+\Delta y,\]то
\[\Delta _{x} z+\Delta _{y} z\ne \Delta z.\]Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Если для каждой совокупности $(x,y,z,...,t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z,...,t)$ в данной области.
Обозначение: $w=f(x,y,z,...,t)$.
Для функции от трех и более переменных, аналогично как для функции двух переменных определяются частные приращения по каждой из переменных:
-
$\Delta _{z} w=f(x,y,z+\Delta z)-f(x,y,z)$ - частное приращение функции $w=f(x,y,z,...,t)$ по $z$;
-
$...$
-
$\Delta _{t} w=f(x,y,z,...,t+\Delta t)-f(x,y,z,...,t)$ - частное приращение функции $w=f(x,y,z,...,t)$ по $t$.
Записать частные и полное приращение функции
\[w=(x+y)\cdot z.\]Решение:
По определению частного приращения найдем:
$\Delta _{x} w=((x+\Delta x)+y)\cdot z$ - частное приращение функции $w=f(x,y,z)$ по $x$
$\Delta _{y} w=(x+(y+\Delta y))\cdot z$ - частное приращение функции $w=f(x,y,z)$ по $y$;
$\Delta _{z} w=(x+y)\cdot (z+\Delta z)$ - частное приращение функции $w=f(x,y,z)$ по $z$;
По определению полного приращения найдем:
$\Delta w=((x+\Delta x)+(y+\Delta y))\cdot (z+\Delta z)$ - полное приращение функции $w=f(x,y,z)$.
Вычислить частные и полное приращение функции $w=xyz$ в точке $(1;2;1)$ при $\Delta x=0,1;\, \, \Delta y=0,1;\, \, \Delta z=0,1$.
Решение:
По определению частного приращения найдем:
$\Delta _{x} w=(x+\Delta x)\cdot y\cdot z$ - частное приращение функции $w=f(x,y,z)$ по $x$
$\Delta _{y} w=x\cdot (y+\Delta y)\cdot z$ - частное приращение функции $w=f(x,y,z)$ по $y$;
$\Delta _{z} w=x\cdot y\cdot (z+\Delta z)$ - частное приращение функции $w=f(x,y,z)$ по $z$;
По определению полного приращения найдем:
$\Delta w=(x+\Delta x)\cdot (y+\Delta y)\cdot (z+\Delta z)$ - полное приращение функции $w=f(x,y,z)$.
Следовательно,
\[\Delta _{x} w=(1+0,1)\cdot 2\cdot 1=2,2\] \[\Delta _{y} w=1\cdot (2+0,1)\cdot 1=2,1\] \[\Delta _{y} w=1\cdot 2\cdot (1+0,1)=2,2\] \[\Delta z=(1+0,1)\cdot (2+0,1)\cdot (1+0,1)=1,1\cdot 2,1\cdot 1,1=2,541.\]С геометрической точки зрения полное приращение функции $z=f(x,y)$ (по определению $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$) равно приращению аппликаты графика функции $z=f(x,y)$ при переходе от точки $M(x,y)$ к точке $M_{1} (x+\Delta x,y+\Delta y)$ (рис. 1).
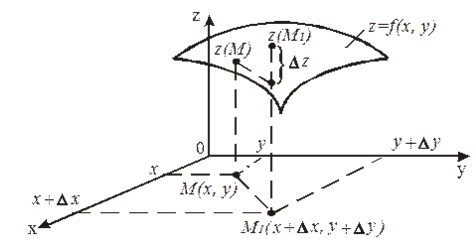
Рисунок 1.











