Если для каждой пары $(x,y)$ значений двух независимых переменных из некоторой области ставится в соответствие определенное значение $z$, то говорят, что $z$ является функцией двух переменных $(x,y)$. Обозначение: $z=f(x,y)$.
В отношении функции $z=f(x,y)$ рассмотрим понятия общего (полного) приращения функции и полного дифференциала.
Пусть дана функция $z=f(x,y)$двух независимых переменных $(x,y)$.
Если аргументу $x$ дать приращение $\Delta x$, а аргументу $y$ -- приращение $\Delta y$, то получается полное приращение заданной функции $z=f(x,y)$. Обозначение:
Записать полное приращение заданной функции
\[z=x+y.\]Решение:
По определению полного приращения некоторой функции найдем:
$\Delta z=x+\Delta x+y+\Delta y$ - полное приращение функции $z=f(x,y)$.
Вычислить полное приращение заданной функции $z=xy$ в точке $(1;2)$ при $\Delta x=0,1;\, \, \Delta y=0,1$.
Решение:
По определению полного приращения некоторой функции найдем:
$\Delta z=(x+\Delta x)\cdot (y+\Delta y)$ - полное приращение функции $z=f(x,y)$.
Следовательно,
\[\Delta z=(1+0,1)\cdot (2+0,1)=1,1\cdot 2,1=2,31.\]Если для каждой тройки $(x,y,z)$ значений трех независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией трех переменных $(x,y,z)$ в данной области.
Обозначение: $w=f(x,y,z)$.
Если для каждой совокупности $(x,y,z,...,t)$ значений независимых переменных из некоторой области ставится в соответствие определенное значение $w$, то говорят, что $w$ является функцией переменных $(x,y,z,...,t)$ в данной области.
Обозначение: $w=f(x,y,z,...,t)$.
Для функции трех и более переменных, аналогично как для функции двух переменных определяются полное приращение:
Записать полное приращение заданной функции
\[w=(x+y)\cdot z.\]Решение:
По определению полного приращения некоторой функции найдем:
$\Delta w=((x+\Delta x)+(y+\Delta y))\cdot (z+\Delta z)$ - полное приращение функции $w=f(x,y,z)$.
Вычислить полное приращение заданной функции $w=xyz$ в точке $(1;2;1)$ при $\Delta x=0,1;\, \, \Delta y=0,1;\, \, \Delta z=0,1$.
Решение:
По определению полного приращения некоторой функции найдем:
$\Delta w=(x+\Delta x)\cdot (y+\Delta y)\cdot (z+\Delta z)$ - полное приращение функции $w=f(x,y,z)$.
Следовательно,
\[\Delta z=(1+0,1)\cdot (2+0,1)\cdot (1+0,1)=1,1\cdot 2,1\cdot 1,1=2,541.\]С геометрической точки зрения полное приращение функции $z=f(x,y)$ (по определению $\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$) равно приращению аппликаты графика функции $z=f(x,y)$ при переходе от точки $M(x,y)$ к точке $M_{1} (x+\Delta x,y+\Delta y)$ (рис. 1).
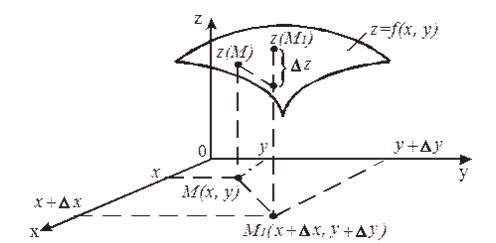
Рисунок 1.
Полный дифференциал заданной функции $z=f(x,y)$ является линейной частью приращения функции и записывается в виде
\[dz=f'_{x} (x,y)\cdot \Delta x+f'_{y} (x,y)\cdot \Delta y.\]Записать полный дифференциал заданной функции
\[z=x+2y.\]Решение:
Определим частные производные заданной функции:
\[f'_{x} (x,y)=1,\, \, f'_{y} (x,y)=2.\]По определению полного дифференциала некоторой функции найдем:
\[dz=1\cdot \Delta x+2\cdot \Delta y=\Delta x+2\cdot \Delta y.\]Вычислить полный дифференциал заданной функции $z=xy$ в точке $(1;2)$ при $\Delta x=0,1;\, \, \Delta y=0,1$.
Решение:
Определим частные производные заданной функции:
\[f'_{x} (x,y)=y,\, \, f'_{y} (x,y)=x.\]По определению полного дифференциала некоторой функции найдем:
\[dz=y\cdot \Delta x+x\cdot \Delta y.\]Следовательно,
\[dz|_{(1,2)} =2\cdot 0,1+1\cdot 0,1=0,2+0,1=0,3.\]Для функции трех и более переменных, аналогично как для функции двух переменных определяются полный дифференциал:
\[dw=f'_{x} (x,y,z)\cdot \Delta x+f'_{y} (x,y,z)\cdot \Delta y+f'_{z} (x,y,z)\cdot \Delta z,\] \[dw=f'_{x} (x,y,z,...,t)\cdot \Delta x+f'_{y} (x,y,z,...,t)\cdot \Delta y+...+f'_{t} (x,y,z,...,t)\cdot \Delta t.\]Записать полный дифференциал заданной функции
\[w=(x+y)\cdot z.\]Решение:
Определим частные производные заданной функции:
\[f'_{x} (x,y,z)=z,\, \, f'_{y} (x,y,z)=z,\, \, \, f'_{z} (x,y,z)=x+y.\]По определению полного дифференциала некоторой функции найдем:
\[dz=z\cdot \Delta x+z\cdot \Delta y+(x+y)\cdot \Delta z.\]Приращения независимых переменных, а именно, $\Delta x,\, \, \Delta y,\, \, \Delta z,...,\Delta t$ называют дифференциалами независимых переменных $x,y,z,...,t$. Обозначение: $dx,dy,dz,...,dt$.
В новых обозначениях выражения для полного дифференциала принимает следующий вид:
Функция, имеющая непрерывные частные производные в заданной точке, является дифференцируемой в данной точке, при этом полный дифференциал функции в данной точке равен сумме произведений частных производных на дифференциалы независимых переменных соответственно.
Записать полный дифференциал заданной функции
\[w=x\cdot z.\]Решение:
Определим частные производные заданной функции:
\[f'_{x} (x,y,z)=z,\, \, f'_{y} (x,y,z)=0,\, \, \, f'_{z} (x,y,z)=x.\]По определению полного дифференциала некоторой функции найдем:
\[dz=z\cdot dx+0\cdot dy+x\cdot dz=z\cdot dx+x\cdot dz.\]Записать полный дифференциал заданной функции $z=xy$ в точке $(1;2)$.
Решение:
Определим частные производные заданной функции:
\[f'_{x} (x,y)=y,\, \, f'_{y} (x,y)=x.\]По определению полного дифференциала некоторой функции найдем:
\[dz=y\cdot dx+x\cdot dy.\]Запишем полный дифференциал в заданной точке:
\[dz|_{(1,2)} =2\cdot dx+1\cdot dy=2dx+dy.\]













