Определение прямой пропорциональности
Для начала напомним следующее определение:
Две величины называются прямо пропорциональными, если их отношение равно конкретному, отличному от нуля числу, то есть:
\[\frac{y}{x}=k\]Отсюда мы видим, что $y=kx$.
Функция вида $y=kx$ называется прямой пропорциональностью.
Прямая пропорциональность является частным случаем линейной функции $y=kx+b$ при $b=0$. Число $k$ называется коэффициентом пропорциональности.
Примером прямой пропорциональности может служить второй закон Ньютона: Ускорение тела прямо пропорционально приложенной к нему силе:
\[F=ma\]Здесь масса -- коэффициент пропорциональности.
Исследование функции прямой пропорциональности $f(x)=kx$ и её график
Вначале рассмотрим функцию $f\left(x\right)=kx$, где $k > 0$.
- Область определения -- все числа.
- Область значения -- все числа.
- $f\left(-x\right)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
- Функция проходит через начало координат.
- $f'\left(x\right)={\left(kx\right)}'=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
- $f^{''}\left(x\right)=k'=0$. Следовательно, функция не имеет точек перегиба.
- ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
- График (рис. 1).
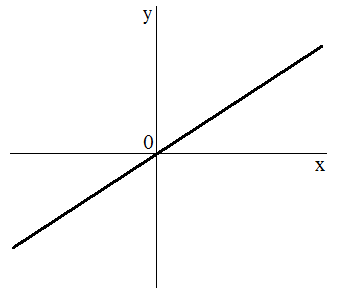
Рис. 1. График функции $y=kx$, при $k>0$
Теперь рассмотрим функцию $f\left(x\right)=kx$, где $k
- Область определения -- все числа.
- Область значения -- все числа.
- $f\left(-x\right)=-kx=-f(x)$. Функция прямой пропорциональности нечетна.
- Функция проходит через начало координат.
- $f'\left(x\right)={\left(kx\right)}'=k
- $f^{''}\left(x\right)=k'=0$. Следовательно, функция не имеет точек перегиба.
- ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
- График (рис. 2).
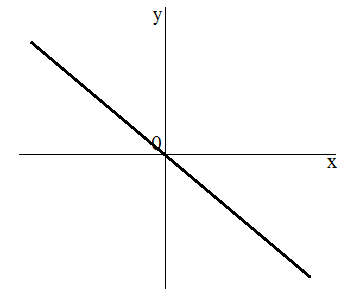
Рис. 2. График функции $y=kx$, при $k
Важно: для построения графика функции $y=kx$ достаточно найти одну, отличную от начала координат точку $\left(x_0,\ y_0\right)$ и провести прямую через эту точку и начало координат.
Задачи на построение графиков функции прямой пропорциональности
Построить график функции $y=-x$
Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=-1$. Проведем прямую через точки $\left(1,-1\right)\ и\ (0,\ 0)$. Получим
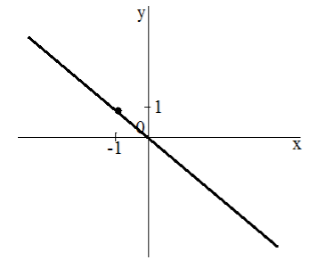
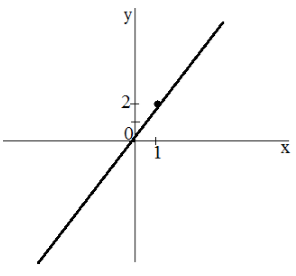
Построить график функции $y=2x$
Найдем точку, принадлежащую данной функции. Пусть $x=1$, тогда $y=2$. Проведем прямую через точки $\left(1,2\right)\ и\ (0,\ 0)$. Получим