Определение линейной функции
Введем определение линейной функции
Функция вида $y=kx+b$, где $k$ отлично от нуля называется линейной функцией.
График линейной функции -- прямая. Число $k$ называется угловым коэффициентом прямой.
При $b=0$ линейная функция называется функцией прямой пропорциональности $y=kx$.
Рассмотрим рисунок 1.
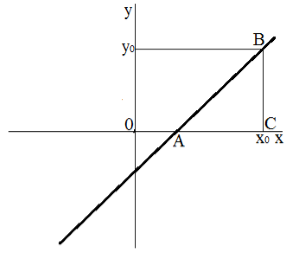
Рис. 1. Геометрический смысл углового коэффициента прямой
Рассмотрим треугольник АВС. Видим, что$ВС=kx_0+b$. Найдем точку пересечения прямой $y=kx+b$ с осью $Ox$:
\[kx+b=0\] \[x=-\frac{b}{k}\]Значит $AC=x_0+\frac{b}{k}$. Найдем отношение этих сторон:
\[\frac{BC}{AC}=\frac{kx_0+b}{x_0+\frac{b}{k}}=\frac{k(kx_0+b)}{{kx}_0+b}=k\]С другой стороны $\frac{BC}{AC}=tg\angle A$.
Таким образом, можно сделать следующий вывод:
Исследование линейной функции $f\left(x\right)=kx+b$ и её график
Вначале рассмотрим функцию $f\left(x\right)=kx+b$, где $k > 0$.
- Область определения -- все числа.
- Область значения -- все числа.
- $f\left(-x\right)=-kx+b$. Функция не является ни четной, ни нечетной.
- При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.
Точки пересечения с осями координат: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$
- $f'\left(x\right)={\left(kx+b\right)}'=k>0$. Следовательно, данная функция возрастает на всей области определения. Точек экстремума нет.
- $f^{''}\left(x\right)=k'=0$. Следовательно, функция не имеет точек перегиба.
- ${\mathop{lim}_{x\to -\infty } kx\ }=-\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=+\infty $
- График (рис. 2).
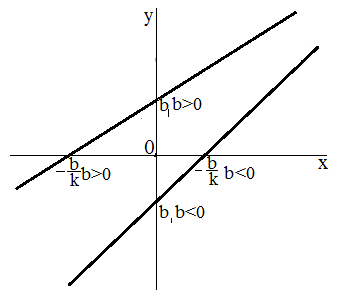
Рис. 2. Графики функции $y=kx+b$, при $k > 0$.
Теперь рассмотрим функцию $f\left(x\right)=kx$, где $k
- Область определения -- все числа.
- Область значения -- все числа.
- $f\left(-x\right)=-kx+b$. Функция не является ни четной, ни нечетной.
- При $x=0,f\left(0\right)=b$. При $y=0,0=kx+b,\ x=-\frac{b}{k}$.
Точки пересечения с осями координат: $\left(-\frac{b}{k},0\right)$ и $\left(0,\ b\right)$
- $f'\left(x\right)={\left(kx\right)}'=k
- $f^{''}\left(x\right)=k'=0$. Следовательно, функция не имеет точек перегиба.
- ${\mathop{lim}_{x\to -\infty } kx\ }=+\infty $, ${\mathop{lim}_{x\to +\infty } kx\ }=-\infty $
- График (рис. 3).
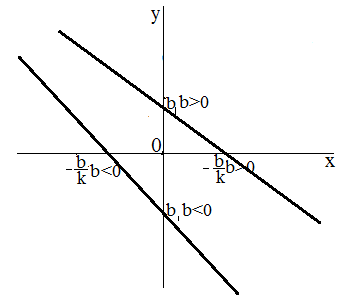
Рис. 3. Графики функции $y=kx+b$, при $k
Важно: для построения графика функции $y=kx$ достаточно найти две точки и провести прямую через эти точки.
Задача на построение графиков функции прямой пропорциональности
Построить график функции $y=2x+3$
Найдем две точки, принадлежащие данной функции. Пусть $x=1$, тогда $y=5$. Пусть $x=-1$, тогда $y=1$. Проведем прямую через точки $\left(-1,1\right)\ и\ (1,\ 5)$. Получим