Формулы для возведения двучлена в $n$-ю степень
Если вспомнить уроки алгебры и математики, то для упрощения вычислений и преобразований различных выражений можно пользоваться заранее выведенными формулами. Одними из таких формул являются формулы возведения двучлена в $n-ю$ степень.
Данные формулы можно вывести с помощью бинома Ньютона.
Формула бинома Ньютона для натуральных чисел имеет следующий вид:
${(a+b)}^n=C^0_na^n+C^1_na^{n-1}b+C^2_na^{n-2}b^2+\dots +C^{n-1}_nab^{n-1}+C^n_nb^n$
Здесь $C^0_n,\ C^1_n,\dots ,C^{n-1}_n,C^n_n$ - коэффициенты Бинома Ньютона.
Коэффициенты разложения Бинома Ньютона можно находить с помощью треугольника Паскаля.
Треугольник Паскаля имеет следующую структуру (таблица 1).

Рисунок 1. Структура треугольника Паскаля. Автор24 — интернет-биржа студенческих работ
Значения коэффициентов треугольника паскаля приведены в следующей таблице:
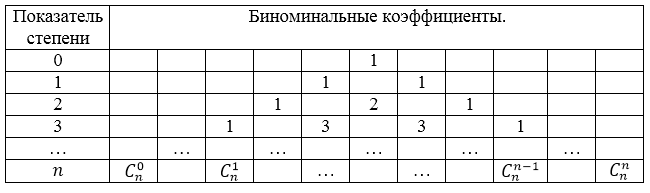
Рисунок 2. Коэффициенты треугольника Паскаля. Автор24 — интернет-биржа студенческих работ
Формулы для вычисления квадратов и кубов суммы и разности
Используя Бином Ньютона можно легко найти формулы для вычисления квадратов и кубов суммы и разности. Получим следующие формулы сокращенного сложения (далее – формулы ФСУ):
Квадрат суммы:
${(a+b)}^2=a^2+2ab+b^2$
Квадрат разности:
${(a-b)}^2=a^2-2ab+b^2$
Куб суммы:
${(a+b)}^3=a^3+3a^2b+3ab^2+b^3$
Куб разности:
${(a-b)}^3=a^3-3a^2b+3ab^2-b^3$
Используя полученные ФСУ, можно выводить также формулы кубов и квадратов трехчленов и многочленов с 4-мя и выше количеством членов. Приведем пример такого вывода. Найдем квадрат суммы трехчлена:
${(a+b+c)}^2$
Для этого сделаем следующую замену. Пусть $a+b=t$, тогда
${(a+b+c)}^2={(t+c)}^2$
Воспользуемся ФСУ квадрата суммы:
${(t+c)}^2=t^2+2tc+c^2$
Вернемся к замене:
${(a+b)}^2+2(a+b)c+c^2$
Вновь воспользуемся формулой a2 b2 сумма квадратов:
${(a+b)}^2+2\left(a+b\right)c+c^2=a^2+b^2+c^2+2ab+2ac+2bc$
Другие формулы сокращенного умножения
Представим еще несколько формул сокращенного умножения.
Разность квадратов двух выражений равна произведению их разность на их сумму:
$\left(a-b\right)\left(a+b\right)=a^2-ab+ab-b^2=a^2-b^2$
Сумма кубов двух выражений а3+b3 равна произведению разности этих выражений на неполный квадрат их суммы:
$\left(a-b\right)\left(a^2+ab+b^2\right)=a^3+a^2b+ab^2-a^2b-ab^2-b^3=a^3-b^3$
Разность кубов двух выражений равна произведению суммы этих выражений на неполный квадрат их разности:
$\left(a+b\right)\left(a^2-ab+b^2\right)=a^3-a^2b+ab^2+a^2b-ab^2+b^3=a^3+b^3$
Примеры задач на применение формул сокр. умножения
Упростить уравнение:
а) ${(x+8)}^2-2\left(x+8\right)\left(x-2\right){+(x-2)}^2$
б) ${(y+7)}^2-2\left(y+1\right)\left(y-1\right){+(y-7)}^2$
в) $\left(a+5\right)\left(a^2-5a+25\right)-a(a^2+3)$
г) $\left(2b-1\right)\left({4b}^2+2b+1\right)-b\left(b-1\right)(b+1)$
Решение:
а) ${(x+8)}^2-2\left(x+8\right)\left(x-2\right){+(x-2)}^2$
Воспользуемся формулой квадрата разности:
${(x+8)}^2-2\left(x+8\right)\left(x-2\right){+(x-2)}^2=$
${=(x+8-x+2)}^2={10}^2=100$
б) ${(y+7)}^2-2\left(y+1\right)\left(y-1\right){+(y-7)}^2$
Воспользуется формулами квадрата суммы и разности, и разности квадратов:
${(y+7)}^2-2\left(y+1\right)\left(y-1\right){+(y-7)}^2=$
$=y^2+14y+49-2y^2+2+y^2-14y+49=100$
в) $\left(a+5\right)\left(a^2-5a+25\right)-a(a^2+3)$
Воспользуемся формулой суммы кубов а3+b3:
$\left(a+5\right)\left(a^2-5a+25\right)-a\left(a^2+3\right)=$
$=a^3+125-a^3-3a=125-3a$
г) $\left(2b-1\right)\left({4b}^2+2b+1\right)-b\left(b-1\right)(b+1)$
Воспользуемся формулой разности кубов и разности квадратов:
$\left(2b-1\right)\left({4b}^2+2b+1\right)-b\left(b-1\right)\left(b+1\right)=$
$={8b}^3-1-b^3+1={7b}^3$












