Понятие параллелограмма
Параллелограмм -- это четырехугольник, в котором противоположные стороны параллельны между собой (рис. 1).
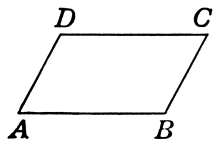
Рисунок 1.
Параллелограмм имеет два основных свойства. Рассмотрим их без доказательства.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Признаки параллелограмма
Рассмотрим три признака параллелограмма и представим их в виде теорем.
Если две стороны четырехугольника равны между собой, а также параллельны, то этот четырехугольник будет параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AB||CD$ и $AB=CD$ Проведем в нем диагональ $AC$ (рис. 2).
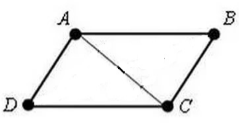
Рисунок 2.
Рассмотрим параллельные прямые $AB$ и $CD$ и их секущую $AC$. Тогда
\[\angle CAB=\angle DCA\]как накрест лежащие углы.
По $I$ признаку равенства треугольников,
\[\triangle DAC=\triangle ACB\]так как $AC$ -- их общая сторона, а $AB=CD$ по условию. Значит
\[\angle DAC=\angle ACB\]Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$.}Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
Теорема доказана.
Если противоположные стороны четырехугольника равны между собой, то он является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AD=BC$ и $AB=CD$. Проведем в нем диагональ $AC$ (рис. 3).
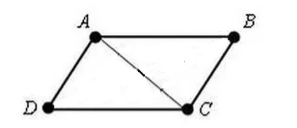
Рисунок 3.
Так как $AD=BC$, $AB=CD$, а $AC$ -- общая сторона, то по $III$ признаку равенства треугольников,
\[\triangle DAC=\triangle ACB\]Тогда
\[\angle DAC=\angle ACB\]Рассмотрим прямые $AD$ и $CB$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AD||CB$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
Также
\[\angle DCA=\angle CAB\]Рассмотрим прямые $AB$ и $CD$ и их секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению 1, данный четырехугольник является параллелограммом.
Теорема доказана.
Если диагонали, проведенные в четырехугольнике, своей точкой пересечения делятся на две равные части, то этот четырехугольник является параллелограммом.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $O$ (рис. 4).
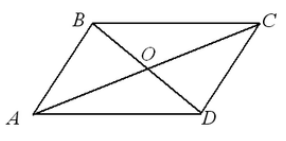
Рисунок 4.
Так как, по условию $BO=OD,\ AO=OC$, а углы $\angle COB=\angle DOA$ как вертикальные, то, по $I$ признаку равенства треугольников,
\[\triangle BOC=\triangle AOD\]Тогда
\[\angle DBC=\angle BDA\]Рассмотрим прямые $BC$ и $AD$ и их секущую $BD$, по последнему равенству накрест лежащих углов получим, что $BC||AD$. Также $BC=AD$. Следовательно, по теореме $1$, данный четырехугольник является параллелограммом.
Теорема доказана.
Пример задачи на признаки параллелограмма
Доказать, что если у четырехугольника $AD||BC$ и $\angle D=\angle B$, то он является четырехугольником.
Доказательство.
Пусть нам дан четырехугольник $ABCD$. В котором $AD||BC$ и $\angle D=\angle B$. Проведем в нем диагональ $AC$ (рис. 5).
Рисунок 5.
Рассмотрим параллельные прямые $AD$ и $BC$ и их секущую $AC$. Тогда
\[\angle DAC=\angle ACB\]как накрест лежащие углы.
\[\angle ACD={180}^0-\angle DAC-\angle D\] \[\angle CAB={180}^0-\angle ACB-\angle B={180}^0-\angle DAC-\angle D=\angle ACD\]Рассмотрим прямые $AB$ и $CD$ и секущую $AC$, по последнему равенству накрест лежащих углов получим, что $AB||CD$. Следовательно, по определению $1$, данный четырехугольник является параллелограммом.
ч. т. д.











