Математическая статистика -- раздел математики, изучающий математические приемы и методы обработки, систематизации и использования статистических данных для каких либо исследований.
Одно из основных понятий математической статистики понятие совокупности. Совокупности можно разделить на генеральную и выборочную.
Генеральная совокупность -- совокупность случайно обобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.
Выборочная совокупность -- часть отобранных объектов из генеральной совокупности.
Одним из способов записи совокупностей -- запись ряда распределения частот, где $x_i$ -- варианта, $n_i$ -- частота данной варианты (таблица 1):
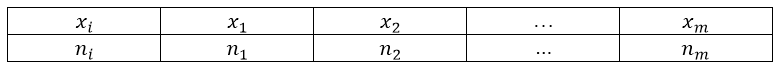
Рисунок 1. Ряд распределения частот.
Также в математической статистике можно столкнуться с понятием относительной частоты, которая находится по формуле: $W_i=\frac{n_i}{n}$
В связи с этим можно построить ряд распределения относительной частоты (таблица 2).
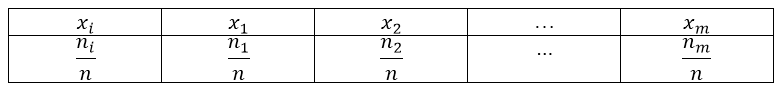
Рисунок 2. Ряд распределения относительных частот.
По рядам распределения можно строить полигоны и гистограммы частот и относительных частот.
Полигон частот -- ломанная, которая соединяет точки $(x_m,n_m)$ ($m=1,2,\dots ,m)$.
Гистограмма частот -- ступенчатая фигура, состоящая из прямоугольников с основанием -- частичными интервалами длины $h$ и высотами $\frac{n_i}{h}$.
Аналогично определяются понятия полигона и гистограммы относительных частот.
Еще одно важное понятие -- эмпирическая функция распределения.
Эмпирической функцией распределения $F_n(x)$ называется функция, которая определяет для каждого значения $x$ относительную частоту события $X \[F_n\left(x\right)=\frac{n_x}{n}\]
где $n_x$ - число вариант, меньших $x$, $n$ -- объем выборки.
Отметим также пару формул для нахождения несмещенных оценок числовых характеристик случайной величины.
- Несмещенная оценка математического ожидания:
- Несмещенная оценка дисперсии:
Из группы заводов одной из областей России случайным образом отобрано 30, по которым получены показатели основных фондов в миллионах рублей: 1, 2, 1, 3, 4, 1, 2, 2, 5, 3, 4, 3, 5, 4, 2, 3, 1, 3, 2, 2, 4, 3, 5, 3, 4, 2, 3, 2, 1, 3.
-
Составить дискретное статистическое распределение выборки.
-
Найти объем выборки.
-
Составить распределение относительных частот.
-
Построить полигон частот.
-
Составить и построить график эмпирической функции распределения.
-
Найти несмещенные оценки числовых характеристик.
Решение:
- Построим таблицу распределения выборки. Для этого в первой строчки запишем все возможные различные значения выборки в порядке возрастания, а во второй строчке посчитаем для каждого такого значения частоту. Получим:

Рисунок 3.
-
Объем выборки: $n=5+8+9+5+3=30$
-
Посчитаем относительные частоты по формуле: $W_i=\frac{n_i}{n}$
Получим следующую таблицу распределения относительной частоты:

Рисунок 4.
Построим полигон частот по определению, обращаясь к таблице из пункта 1.
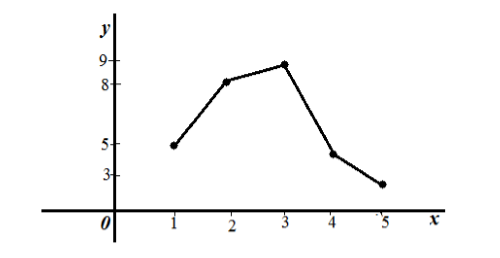
Рисунок 5.
Имеем при $x\le 1$ $F_n\left(x\right)=0$, а при $x>5$ $F_n\left(x\right)=1$.
Значение $x
Значение $x
Значение $x
Значение $x
Таким образом, получаем:
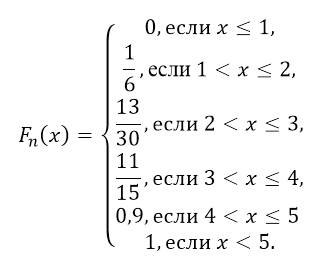
Рисунок 6.
Построим график эмпирического распределения:
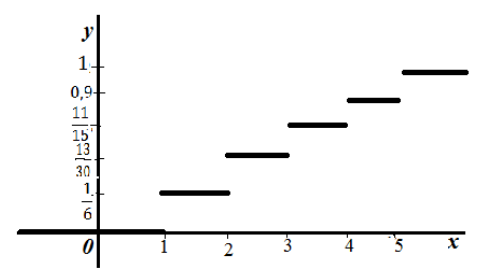
Рисунок 7.
- Несмещенная оценка математического ожидания:
\end{enumerate}
Несмещенная оценка дисперсии:
\[D_В=\overline{x^2_В}-({\overline{x_В})}^2=\frac{\sum\limits^m_{i=1}{n_ix^2_i}}{n}-({\overline{x_В})}^2=\frac{20+72+144+125+108}{30}-{\left(\frac{113}{30}\right)}^2\approx 1,42.\]











