Бесконечные десятичные дроби
Десятичные дроби после запятой могут содержать бесконечное количество цифр.
Бесконечные десятичные дроби -- это десятичные дроби, в записи которых находится бесконечное число цифр.
Бесконечную десятичную дробь практически невозможно записать полностью, поэтому при их записи ограничиваются только некоторым конечным количеством цифр после запятой, после чего ставят многоточие, которое указывает на бесконечно продолжающуюся последовательность цифр.
Например, $0,443340831\dots ; 3,1415935432\dots ; 135,126730405\dots ; 4,33333333333\dots ; 676,68349349\dots$.
Рассмотрим последние две бесконечные десятичные дроби. В дроби $4,33333333333\dots$ бесконечно повторяется цифра $3$, а в дроби $676,68349349\dots$ с третьего знака после запятой повторяется группа цифр $3$, $4$ и $9$. Подобные бесконечные десятичные дроби называются периодическими.
Периодические десятичные дроби
Периодические десятичные дроби (или периодические дроби) -- это бесконечные десятичные дроби, в записи которых с некоторого знака после запятой бесконечно повторяется какая-нибудь цифра или их группа, которая называется периодом дроби}.
Например, период периодической дроби $4,33333333333\dots$ -- цифра $3$, а период дроби $676,68349349\dots$ -- группа цифр $349$.
Для краткости записи бесконечных периодических десятичных дробей принято период записывать один раз, заключив его в круглые скобки. Например, периодическую дробь $4,33333333333\dots$ записывают $4,(3)$, а периодическую дробь $676,68349349\dots$ записывают $676,68(349)$.
Бесконечные десятичные периодические дроби получают при переводе обыкновенных дробей, знаменатели которых содержат простые множители, кроме $2$ и $5$, в десятичные дроби.
Любая конечная десятичная дробь (и целое число) может быть записана в виде периодической дроби, для чего достаточно справа дописать бесконечное количество цифр $0$.
Например, конечная десятичная дробь $45,12$ может быть записана в виде периодической дроби как $45,12(0)$, а целое число $(74)$ в виде бесконечной периодической десятичной дроби будет иметь вид $74(0)$.
В случае периодических дробей, которые имеют период 9, используют переход к другой записи периодической дроби с периодом $0$. Только для этого период 9заменяют периодом $0$, при этом значение следующего по старшинству разряда увеличивается на $1$.
Например, периодическую дробь $7,45(9)$ можно заменить периодической дробью $7,46(0)$ или равной ей десятичной дробью $7,46$.
Бесконечные десятичные периодические дроби представляются рациональными числами. Другими словами, любая периодическая дробь может быть переведена в обыкновенную дробь, а любая обыкновенная дробь может быть представлена в виде периодической дроби.
Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби
В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями $10, 100, \dots$.
В некоторых случаях исходную обыкновенную дробь можно легко привести к знаменателю $10$, $100$ или $1 \ 000$, после чего можно полученную дробь представить в виде десятичной дроби.
Чтобы дробь $\frac{3}{5}$ }привести к дроби со знаменателем $10$, нужно числитель и знаменатель дроби умножить на $2$, после чего получим $\frac{6}{10}$, которую не составит труда перевести в десятичную дробь $0,6$.
Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную}:
-
числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;
-
разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).
Перевести обыкновенную дробь $\frac{621}{4}$ в десятичную дробь.
Решение.
Число $621$ в числителе представим в виде десятичной дроби. Для этого добавим десятичную запятую и для начала два нуля после нее. Далее при необходимости можно буде добавить нули еще. Итак, получили $621,00$.
Выполним деление числа $621,00$ на $4$ в столбик:
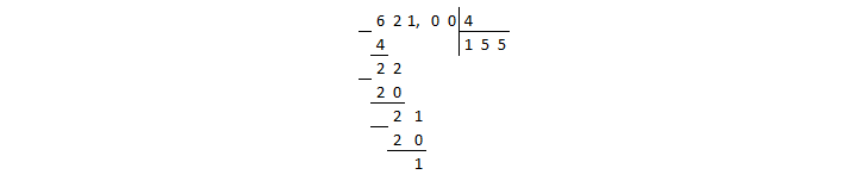
Рисунок 1.
Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:
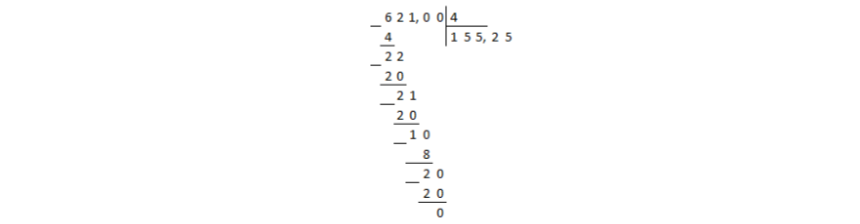
Рисунок 2.
В остатке получили нуль, значит деление окончено.
Ответ: $155,25$.
Возможен случай, когда при делении числителя и знаменателя обыкновенной дроби в остатке $0$ так и не получается. В этом случае деление можно продолжать бесконечно. Начиная с определенного момента остатки от деления периодически повторяются, а значит повторяются и цифры в частном. Из этого можно сделать вывод, что данная обыкновенная дробь переведется в бесконечную периодическую десятичную дробь.
Перевести обыкновенную дробь $\frac{19}{44}$ в десятичную дробь.
Решение.}
Для перевода обыкновенной дроби в десятичную выполним деление в столбик:

Рисунок 3.
При делении повторяются остатки $8$ и $36$, а в частном также повторяются цифры $1$ и $8$. Итак, исходную обыкновенную дробь $\frac{19}{44}$ перевели в периодическую дробь $\frac{19}{44}=0,43181818\dots =0,43(18)$.
Ответ: $0,43(18)$.
Общий вывод о переводе обыкновенных дробей в десятичные:
-
если знаменатель можно разложить на простые множители, среди которых будут присутствовать только числа $2$ и $5$, то такую дробь можно перевести в конечную десятичную дробь;
-
если кроме чисел $2$ и $5$ в разложении знаменателя присутствуют другие простые числа, то такая дробь переводится в бесконечную десятичную периодическую дробь.














