Умножение и деление натуральных чисел. Таблица умножения

Умножение натуральных чисел

Результат умножения натуральных чисел называют их произведением. Произведение двух натуральных чисел $a$ и $b$ содержит стольких единиц, сколько их содержится в числе $a$, взятых столько раз, сколько единиц содержится в числе $b$.

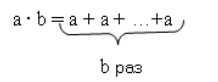
Рисунок 1.

Если произведение обозначить $c$, то говорят, что оно получено в результате умножения чисел $a$ и $b$. Записывается умножение двух чисел следующим образом:

$a\cdot b=c$ или $a\times b=c$.

Числа $n$ и $m$ называют множителями или сомножителями.

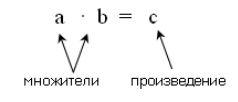
Рисунок 2.

Например, найдем произведение чисел $13\cdot 5$.

По определению операции умножения:

Свойства умножения натуральных чисел

Умножение натуральных чисел характеризуется следующими свойствами:

1. Коммутативность умножения:

   $$a\cdot b=b\cdot a.$$

2. Ассоциативность умножения:

   $$\left(a\cdot b\right)\cdot c=a\cdot \left(b\cdot c\right)$$
   Пример 1

   Например, найдем произведение чисел $9\cdot 15\cdot 6$.

   Применим к данному произведению свойство ассоциативности умножения:

   $$9\cdot 15\cdot 6=9\cdot \left(15\cdot 6\right)=9\cdot 90=810$$

   Из свойства ассоциативности умножения натуральных чисел выводится понятие натуральной степени натурального числа:

   Натуральное число m в степени n равно натуральному числу $k$, которое получается в результате умножения числа $m$ самого на себя $n$ раз:

   
   
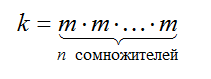
   Рисунок 3.

   Для обозначения $n$-й степени числа m используют запись $m^n$, в которой число $m$ называется основанием степени, а число $n$ - показателем степени.

   Пример 2

   Например, найдем значение выражения $3^4$.

   По определению натуральной степени натурального числа данное выражение можно записать так:

   $$3^4=3\cdot 3\cdot 3\cdot 3=81.$$

   Получили $3^4=81$.

3. Закон дистрибутивности умножения относительно сложения:

   $$\left(a+b\right)\cdot c=a\cdot c+b\cdot c.$$

4. Закон дистрибутивности умножения относительно вычитания:

   $$\left(a-b\right)\cdot c=a\cdot c-b\cdot c.$$

   В результате нахождения суммы и произведения двух натуральных чисел всегда получится натуральное число.

5. Свойство умножения на единицу:

   $$a\cdot 1=1\cdot a=a.$$

6. Свойство умножения на нуль:

   $$a\cdot 0=0\cdot a=0.$$

7. Свойство умножения нулей:

   $$0\cdot 0=0.$$

8. Свойство умножения единиц:

   $$1\cdot 1=1.$$

   Операцию умножения натуральных чисел удобно выполнять «в столбик»:

   
   
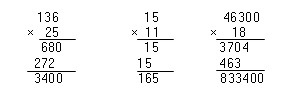
   Рисунок 4.

Деление натуральных чисел

Операция деления натуральных чисел является обратной операцией к умножению.

Результат деления натуральных чисел называют их частным.

Если $b\cdot c=a$, то

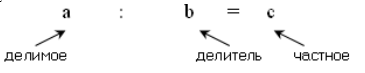
Рисунок 5.

Свойства деления натуральных чисел

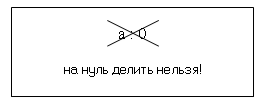
Рисунок 6.

1. Свойство деления произведения на число:

   $$\left(a\cdot b\right):c=\left(a:c\right)\cdot b,$$ $$\left(a\cdot b\right):c=\left(b:c\right)\cdot a,$$ $$\left(a\cdot b\right):c=a:\left(b\cdot c\right).$$

2. Свойство деления на единицу:

   $$a:1=a.$$

3. Свойство деления двух равных натуральных чисел:

   $$a:a=1, a\ne 0.$$

4. Свойство деления нуля на натуральное число:

   $$0:a=0, a\ne 0.$$

   Выполнять деление двух натуральных чисел удобно методом «угла»:

   
   
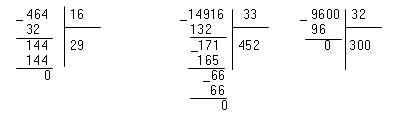
   Рисунок 7.

   В результате нахождения разницы и при делении натуральных чисел натуральное число можно получить не для любой пары натуральных чисел.

   Пример 3

   Например, числа $15$ и $5$ -- натуральные. Результат вычитания $15-5=10$ также будет натуральным числом, а если найти разницу натуральных чисел $5-15=-10$, то получим число, которое уже не является натуральным.

Таблица умножения натуральных чисел

По определению произведения двух натуральных чисел можно получить результаты умножения однозначных натуральных чисел. Например, произведение $5\cdot 4$ равно сумме $4$ одинаковых слагаемых, которые равны $5$. В таком случае получаем $5\cdot 4=5+5+5+5=20$. Аналогично можно получить результат произведений всех однозначных натуральных чисел и записать их в таблицу.

Результаты произведений удобно представлять в виде так называемой таблицы умножения.

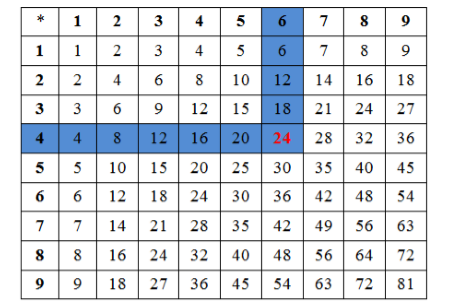
Рисунок 8.

Правила пользования таблицей умножения

Аналогично можно найти произведение остальных чисел, но принято знать таблицу умножения наизусть.