Среднее квадратическое отклонением $\sigma \xi \, $ случайной величины $\xi$ это арифметический корень из ее дисперсии, то есть,
\[\sigma \xi =\sqrt{D\xi } .\]Математическое ожидание это характеристика его среднего значения, дисперсия -- мера рассеивания ее значений вокруг среднего.
Свойства среднего квадратического отклонения
- Среднее квадратическре отклонение постоянной величины равно нулю
- Сталый множитель можно вынести за знак среднего квадратического отклонения.
- Среднеее квадратическое отклонение суммы или разности двух независимых случайных величин равна квадратному корню от суммы увадратов квадратических отклонений этих величин.
Применение на практике
Случайная величина $\xi$ задана плотностью:
\[\rho _{\xi } (x)=\left\{\begin{array}{l} {{\rm \; \; }0,{\rm \; \; \; \; \; \; }x2.} \end{array}\right. \, .\]Требуется:
-
найти коэффициент а, функцию распределения $F_{\xi } (x)$; построить графики $F_{\xi } (x)\, $ и $\rho _{\xi } (x)$;
-
найти $M\xi $, $D\xi $, $\sigma \xi $.
вычислить $P(1,5
Построим график плотности распределения вероятностей случайной величины $\xi$ (рис. 1).
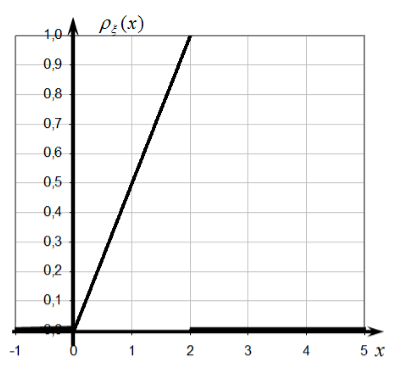
Рисунок 1.
Найдем функцию распределения $F_{\xi } (x)$, имеем $F_{\xi } (x)=\int \limits _{-\infty }^{x}\rho _{\xi } (t) dt\, $. Плотность распределения вероятностей случайной величины $\xi$ определена различными элементарными функциями на трех интервалах, будем фиксировать x в каждом из этих интервалов.
Пусть $x
$0\le x\le 2$, тогда
\[F_{\xi } (x)=\int \limits _{-\infty }^{x}\rho _{\xi } (t) dt=\int \limits _{-\infty }^{0}0 dt+\int \limits _{0}^{x}\frac{t}{2} dt=0+\frac{t^{2} }{4} \left|\begin{array}{c} {^{x} } \\ {_{0} } \end{array}=\frac{x^{2} }{4} \right. ;\]$x>2$, тогда
\[F_{\xi } (x)=\int \limits _{-\infty }^{x}\rho _{\xi } (t) dt=\int \limits _{-\infty }^{0}0 dt+\int \limits _{0}^{2}\frac{t}{2} dt+\int \limits _{2}^{x}0 dt=0+\frac{t^{2} }{4} \left|\begin{array}{c} {^{2} } \\ {_{0} } \end{array}+0=1\right. \, .\]Имеем
\[F_{\xi } (x)=\left\{\begin{array}{l} {{\rm \; \; }0,{\rm \; \; \; \; \; \; }x2.} \end{array}\right. \, \]Построим график функции распределения случайной величины $\xi$ (рис. 2).
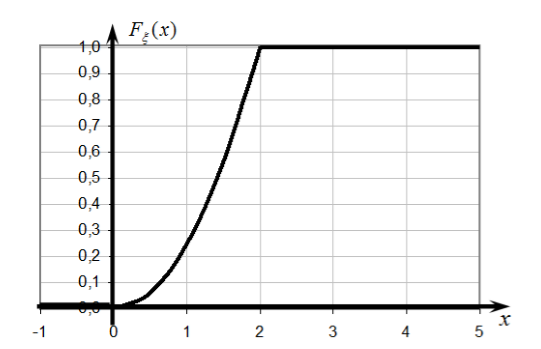
Рисунок 2.
Найдем (по определению) математическое ожидание, дисперсию и среднее квадратичное отклонение
\[M\xi =\int \limits _{-\infty }^{+\infty }x\cdot \rho _{\xi } (x) dx=\int \limits _{-\infty }^{0}x\cdot 0 dx+\int \limits _{0}^{2}x\cdot \frac{x}{2} dx+\int \limits _{2}^{+\infty }x\cdot 0 dx=\frac{1}{2} \cdot \int \limits _{0}^{2}x^{2} dx=\, \] \[=\frac{x^{3} }{6} \left|\begin{array}{c} {^{2} } \\ {_{0} } \end{array}=\frac{8-0}{6} =\frac{4}{3} \right. \, ;\] \[D\xi =\int \limits _{-\infty }^{+\infty }x^{2} \cdot \rho _{\xi } (x) dx-M^{2} \xi =\int \limits _{-\infty }^{0}x^{2} \cdot 0 dx+\int \limits _{0}^{2}x^{2} \cdot \frac{x}{2} dx+\int \limits _{2}^{+\infty }x^{2} \cdot 0 dx-\, \] \[-\left(\frac{4}{3} \right)^{2} =\frac{1}{2} \cdot \int \limits _{0}^{2}x^{3} dx=\frac{x^{4} }{8} \left|\begin{array}{c} {^{2} } \\ {_{0} } \end{array}-\frac{16}{9} =\frac{2^{4} -0}{8} -\frac{16}{9} =\frac{16}{8} -\frac{16}{9} =16\cdot \left(\frac{1}{8} -\frac{1}{9} \right)=\right. \, =16\cdot \frac{9-8}{72} =\frac{16}{72} =\frac{4}{18} =\frac{2}{9} \, ;\] \[\sigma \xi =\sqrt{D\xi } =\sqrt{\frac{2}{9} } =\frac{\sqrt{2} }{3} \approx 0,471\, .\]Вычислим $P(1,5P(1,5












