Математическим ожиданием дискретной случайной величины называется сумма произведений всех ее возможных значений на соответствующие им вероятности:
\[{\rm M} \left({\rm X}\right)=\sum \limits _{i=1}^{n}x_{i} p_{i} {\rm .} \]Дисперсией (рассеиванием) случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
\[D\left(X\right)=M\left(\left(X-M\left(X\right)\right)^{2} \right).\]Обобщением рассмотренных нами числовых характеристик случайной величины являются начальные и центральные моменты $k$-го порядка.
Начальным моментом $k$-го порядка случайной величины $X$ называется математическое ожидание случайной величины $X^{k} $:
Для дискретной случайной величины имеем:
или
если множество значений случайной величины бесконечно, и ряд в правой части сходится абсолютно.
Для непрерывной случайной величины $X$
если несобственный интеграл в правой части сходится; $f(x)$ - плотность распределения вероятностей $X$.
Математическое ожидание есть начальный момент первого порядка:
Центральным моментом $k$-го порядка случайной величины $X$ называется математическое ожидание $k$-ой степени соответствующей центрированной случайной величины $\mathop{X^{k} }\limits^{} \, $:
Для дискретной случайной величины имеем:
или
если множество значений случайной величины бесконечно, и ряд в правой части сходится абсолютно.
Для непрерывной случайной величины $X$
если несобственный интеграл в правой части сходится; $f(x)$ - плотность распределения вероятностей $X$.
Отметим, что $\mu _{1} (X)=0$ для любой случайной величины $X$, а центральный момент второго порядка представляет собой дисперсию:
Если плотность распределения случайной величины $X$ симметрична относительно математического ожидания, то все её центральные моменты нечетных порядков обращаются в нуль. На этом свойстве основывается использование $\mu _{3} (X)$ в качестве характеристики ассиметрии распределения. Для того, чтобы избавиться от кубической размерности, поделим его на $\sigma ^{3} (X)$:
Это так называемый коэффициент ассиметрии или скошенности.
Если кривая плотности распределения непрерывной случайной величины такова, что справа от моды расположена ее «длинная часть», а слева -- «короткая», то коэффициент асимметрии $S_{k} $ положителен.
Коэффициент асимметрии $S_{k} $ отрицателен, если «длинная часть» кривой распределения расположена слева от моды (рис. 1).
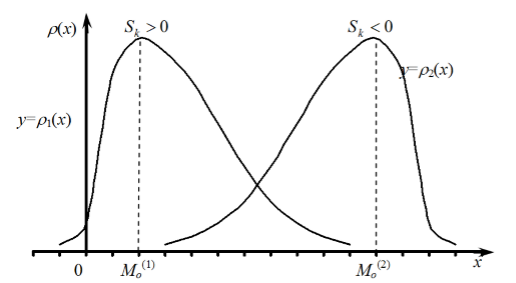
Рисунок 1.
Отношение центрального момента четвертого порядка $\mu _{4} (X)$ к $\sigma ^{4} (X)$ называется эксцессом и служит характеристикой "плосковершинности" графика плотности распределения случайной величины $X$:
Моменты более высоких порядков используются редко.
Использование на практике
Дан возможные значения дискретной случайной величины $\xi$: $x_{1} =-1\, $, $x_{2} =0\, $, $x_{3} =1\, $, а также известно математическое ожидание этой величины и ее квадрат: $M\xi =0,1\, $; $M(\xi ^{2} )=0,9\, $. Найти вероятность $p_{1} \, $, $p_{2} ,$ $p_{3} ,$ соответствующие возможным значениям $x_{1} $, $x_{2} $, $x_{3} $.
Решение.
Запишем таблицу расспределения нешей (рис. 2) случайной величины $\xi$:
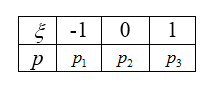
Рисунок 2.
Используя определение математического ожидания дискретной случайной величины и начальный момент второго порядка, получим два уравнения:
\[\left\{\begin{array}{l} {-p_{1} +p_{3} =0,1;} \\ {p_{1} +p_{3} =0,9.} \end{array}\right. \, \]Когда решить систему двух уравнений с двумя неизвестными, получим $p_{1} =0,4$, $p_{3} =0,5$. Так как сумма вероятностей, которые входят в ряд распределения равна 1, то найдем $p_{2} $:
\[p_{2} =1-p_{1} -p_{3} =1-0,4-0,5=0,1\, .\]Найденые значения запишем в таблицу расспределения случайной величины $\xi$:
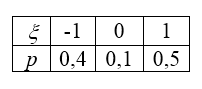
Рисунок 3.












