Какими бывают функции?
Чтобы не заблудиться среди огромного разнообразия функций, очень важно выделить признаки той их части, которая называется алгебраическими функциями.
Прежде всего определимся с элементарными функциями.
Любая функция $f$ считается элементарной, если она задана одним уравнением $y=f\left(x\right)$, составленным из основных элементарных функций с помощью конечного числа арифметических действий и композиций.
В определении применены следующие понятия:
-
Это значит, что над двумя данными произвольными функциями $u\left(x\right)$ и $v\left(x\right)$ в данной области определения можно выполнять сложение $u\left(x\right)+v\left(x\right)$, вычитание $u\left(x\right)-v\left(x\right)$, умножение $u\left(x\right)\cdot v\left(x\right)$, а также деление $\frac{u\left(x\right)}{v\left(x\right)} $. При делении предполагается, что для всех $x$ из данной области определения выполняется условие $v\left(x\right)\ne 0$.
-
Операция композиции
Операция композиции состоит в следующем. Пусть $y$ является функцией от $u$, то есть $y=f\left(u\right)$. Пусть также в свою очередь, $u$ является функцией независимой переменной $x$, то есть $u=g\left(x\right)$. В этих условиях функция $y=f\left(g\left(x\right)\right)$ называется композицией данных функций $f$ и $g$.
Функция $y=\frac{x\cdot 3^{x} }{\sqrt{2-\cos x} } +\arcsin ^{2} x$ является элементарной. В ней использованы все четыре арифметических действия, основные элементарные функции (постоянная, степенная, показательная, тригонометрическая и обратная тригонометрическая), а также представлены композиции функций в виде $\arcsin ^{2} x$ и $\sqrt{2-\cos x} $.
Все элементарные функции распределяют на алгебраические и трансцендентные (те, которые к алгебраическим не относятся).
Разновидности алгебраических функций
Существует три основных разновидности алгебраических функций.
Целые рациональные функции (многочлены, полиномы)
Это функции вида $y=P\left(x\right)=a_{n} \cdot x^{n} +a_{n-1} \cdot x^{n-1} +\ldots +a_{1} \cdot x+a_{0} $, где $a_{0} ,\; a_{1} ,\; \ldots ,\; a_{n} $ -- постоянные действительные числа, называемые коэффициентами, $n$ -- целое неотрицательное число. Если $a_{n} \ne 0$, то $n$ называют степенью многочлена.
Многочлен второй степени $y=3\cdot x^{2} -x+5$. Многочлен нулевой степени $y=7$.
Дробно-рациональные функции (рациональные дроби)
Это функции вида $y=\frac{P\left(x\right)}{Q\left(x\right)} =\frac{a_{n} \cdot x^{n} +a_{n-1} \cdot x^{n-1} +\ldots +a_{1} \cdot x+a_{0} }{b_{m} \cdot x^{m} +b_{m-1} \cdot x^{m-1} +\ldots +b_{1} \cdot x+b_{0} } $, представляющие собой отношение двух многочленов.
Рациональная дробь $y=\frac{x^{2} +1}{7\cdot x^{3} +4\cdot x-2} $.
Иррациональные функции
В состав таких функций входят рациональные функции с нецелыми рациональными показателями степени при использовании арифметических действий. Внешний признак иррациональной функции -- наличие корней различной степени.
Иррациональная функция $y=3-\sqrt[{5}]{x^{2} } +\sqrt{\frac{x+1}{x^{2} -1} } $.
Свойства рациональных дробей
Дана рациональная дробь $\frac{P\left(x\right)}{Q\left(x\right)} =\frac{a_{n} \cdot x^{n} +a_{n-1} \cdot x^{n-1} +\ldots +a_{1} \cdot x+a_{0} }{b_{m} \cdot x^{m} +b_{m-1} \cdot x^{m-1} +\ldots +b_{1} \cdot x+b_{0} } $, где $P\left(x\right)$ и $Q\left(x\right)$ -- многочлены. Пусть коэффициенты $a_{n} \ne 0$ и $b_{m} \ne 0$. Тогда указанные многочлены имеют степени $n$ и $m$ соответственно. Данная рациональная дробь определена во всех точках числовой оси, за исключением тех точек, в которых знаменатель $Q\left(x\right)=0$.
Рациональную дробь называют правильной, если степень числителя меньше степени знаменателя, то есть $n Если рациональная дробь является неправильной, то посредством деления числителя $P\left(x\right)$ на знаменатель $Q\left(x\right)$ её можно представить в виде$\frac{P\left(x\right)}{Q\left(x\right)} =M\left(x\right)+\frac{R\left(x\right)}{Q\left(x\right)} $ или $P\left(x\right)=M\left(x\right)\cdot Q\left(x\right)+R\left(x\right)$, где $\frac{R\left(x\right)}{Q\left(x\right)} $ -- правильная рациональная дробь, а многочлены $M\left(x\right)$ и $R\left(x\right)$ -- соответственно частное и остаток от деления многочленов. При этом сумма степеней многочленов $M\left(x\right)$ и $Q\left(x\right)$ равна степени многочлена $P\left(x\right)$. Деление рациональных дробей
Разделить многочлены $\frac{3\cdot x^{4} -2\cdot x^{3} -x^{2} +7\cdot x-5}{x^{2} -2\cdot x+3} $.
Деление в данном случае возможно, так как степень числителя (четвёртая) больше степени знаменателя (вторая). Деление многочленов выполняем "углом".
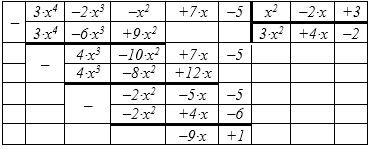
Результат деления имеет следующий вид:
\[\frac{3\cdot x^{4} -2\cdot x^{3} -x^{2} +7\cdot x-5}{x^{2} -2\cdot x+3} =3\cdot x^{2} +4\cdot x-2+\frac{-9\cdot x+1}{x^{2} -2\cdot x+3} .\] Здесь $M\left(x\right)=3\cdot x^{2} +4\cdot x-2$ -- частное от деления, $R\left(x\right)=-9\cdot x+1$ -- остаток от деления.Сокращение рациональных дробей
Рациональная дробь $\frac{P\left(x\right)}{Q\left(x\right)} $, как и числовая, бывает сократимой или несократимой. Предположим, что данная рациональная дробь является сократимой, так как оба многочлена $P\left(x\right)$ и $Q\left(x\right)$ имеют общие множители, содержащие переменную $x$. Произведение всех этих множителей называется наибольшим общим делителем данных многочленов, то есть $P\left(x\right)=N\left(x\right)\cdot P_{1} \left(x\right)$ и $Q\left(x\right)=N\left(x\right)\cdot Q_{1} \left(x\right)$, где многочлен $N\left(x\right)$ -- наибольший общий делитель. В этом случае данная рациональная дробь приобретает вид $\frac{P\left(x\right)}{Q\left(x\right)} =\frac{N\left(x\right)\cdot P_{1} \left(x\right)}{N\left(x\right)\cdot Q_{1} \left(x\right)} =\frac{P_{1} \left(x\right)}{Q_{1} \left(x\right)} $, где рациональная дробь $\frac{P_{1} \left(x\right)}{Q_{1} \left(x\right)} $ является несократимой, а многочлены $P_{1} \left(x\right)$ и $Q_{1} \left(x\right)$ называются взаимно простыми. Если многочлен $N\left(x\right)$ -- какой-то один наибольший общий делитель, то многочлены $C\cdot N\left(x\right)$, где $C$ -- произвольная константа, тоже будут наибольшими общими делителями. Общим делителем взаимно простых многочленов может считаться произвольная константа.
Наибольший общий делитель многочленов $P\left(x\right)$ и $Q\left(x\right)$ можно найти с помощью алгоритма Евклида:
- пусть $U\left(x\right)$ и $V\left(x\right)$ -- это новые обозначения многочленов $P\left(x\right)$ и $Q\left(x\right)$, причем $U\left(x\right)$ -- это тот, который имеет большую степень;
- делим многочлен $U\left(x\right)$ на многочлен $V\left(x\right)$ и получаем $\frac{U\left(x\right)}{V\left(x\right)} =M\left(x\right)+\frac{P\left(x\right)}{V\left(x\right)} $, где новый многочлен $P\left(x\right)$ представляет собой остаток от деления;
- обозначаем многочлен $V\left(x\right)$ как $Q\left(x\right)$ и возвращаемся на шаг 1.
Выполнение данного алгоритма повторяем, пока на шаге 2 не будет достигнуто нулевое значение остатка от деления $P\left(x\right)=0$. Тогда предпоследний, отличный от нуля остаток от деления, будет наибольшим общим делителем данных многочленов $P\left(x\right)$ и $Q\left(x\right)$.
Если полученный по алгоритму Евклида наибольший общий делитель будет иметь вид многочлена $N\left(x\right)$, зависящего от $x$, то данную рациональную дробь $\frac{P\left(x\right)}{Q\left(x\right)} $ можно сократить посредством деления и числителя, и знаменателя на $N\left(x\right)$. Если же наибольший общий делитель будет получен в виде константы, то данную рациональную дробь $\frac{P\left(x\right)}{Q\left(x\right)} $ следует считать несократимой.
Сократить рациональную дробь $\frac{P\left(x\right)}{Q\left(x\right)} =\frac{x^{2} +x-6}{x^{3} +2\cdot x^{2} -4\cdot x-3} $.
Сначала по алгоритму Евклида находим наибольший общий делитель многочленов $P\left(x\right)$ и $Q\left(x\right)$.
Шаг 1. Новые обозначения многочленов $P\left(x\right)$ и $Q\left(x\right)$:
\[U\left(x\right)=x^{3} +2\cdot x^{2} -4\cdot x-3; V\left(x\right)=x^{2} +x-6.\]Шаг 2. Результат деления многочленов:
$\frac{U\left(x\right)}{V\left(x\right)} =\frac{x^{3} +2\cdot x^{2} -4\cdot x-3}{x^{2} +x-6} =x+1+\frac{x+3}{x^{2} +x-6} $, где новый многочлен $P\left(x\right)=x+3$ представляет собой остаток от деления.
Переобозначаем $Q\left(x\right)=x^{2} +x-6$ и возвращаемся на шаг 1.
Шаг 1. Новые обозначения многочленов $P\left(x\right)$ и $Q\left(x\right)$:
\[U\left(x\right)=x^{2} +x-6; V\left(x\right)=x+3.\]Шаг 2. Результат деления многочленов: $\frac{U\left(x\right)}{V\left(x\right)} =\frac{x^{2} +x-6}{x+3} =x-2$, где остаток от деления $P\left(x\right)=0$.
Таким образом, наибольший общий делитель -- это предыдущий, отличный от нуля остаток, то есть $N\left(x\right)=x+3$. Этот наибольший общий делитель представляет собой многочлен, зависящий от $x$, следовательно, сокращение данной рациональной дроби возможно:
\[\frac{P\left(x\right)}{Q\left(x\right)} =\frac{x^{2} +x-6}{x^{3} +2\cdot x^{2} -4\cdot x-3} =\frac{x-2}{x^{2} -x-1} .\]










