Правила построения возмущенных орбиталей супермолекулы
Односторонний Процесс, протекающий в одностороннем порядке между молекулой донора (Д) и моолекулой акцептора (А) можно выразить схемой:
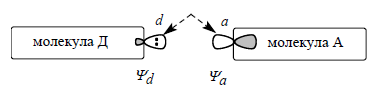
Рисунок 1.
Пунктирной стрелкой на схеме обозначено двустороннее возмущение орбиталей, локализованных на атоме $d$ молекулы донора и атоме $a$ молекулы акцептора.
При образовании комплекса донор -- акцептор, возмущение молекулярных орбиталей протекает подобно возмущению атомных орбиталей при получении молекулы из атомов. Орбитали комплекса донор -- акцептор являются линейной комбинацией взаимодействующих орбиталей донора и акцептора.
При возмущении орбиталей $\psi_a$ и $\psi_d$ появляются две возмущенные орбитали $\psi $+ и $\psi $-, которые относятся к супермолекуле акцептор $\leftarrow$ донор.
Правила построения возмущенных орбиталей супермолекулы:
-
При формировании возмущенной нижней орбитали соединяются исходные орбитали с одинаковыми знаками, и в районе их взаимодействия происходит связывание. При формировании возмущенной верхней орбитали происходит объединение исходных орбиталей с разными знаками, в результате чего наблюдается антисвязывание:
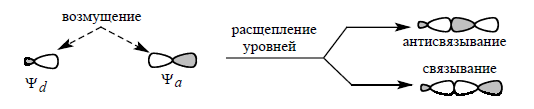
Рисунок 2.Обозначим энергию орбитали $\psi_d$ как $a_d$, энергию $\psi_a$ - как $a_a$, пусть $E$ обозначает энергии возмущения орбиталей $\psi $+ и $\psi $-.
Согласно теории возмущений,
\[\left(a_d-E\right)\left(a_a-E\right)={(\beta -SE)}^2,\]где $\beta $ --резонансный интеграл, который характеризует силу взаимодействия $\psi_a$ и $\psi_d$ на данном расстоянии; $S$ -- интеграл перекрывания, показывающий степень перекрывания взаимодействующих орбиталей.
При образовании возмущенных орбиталей, которые значительно отличаются величиной энергии, используют следующие правила:
-
Если невозмущенные орбитали обладают разной энергией, то у орбитали, имеющей первоначально более низкую энергию, энергия еще сильнее понижается, а у орбитали с более высокой энергией, энергия повышается. Эти изменения тем сильнее выражены, чем лучше перекрывание, и тем менее проявлены, чем больше первоначальное различие между энергиями орбиталей.
-
Орбиталь, имеющая первоначально более низкую энергию, будет меняться в результате частичного подмешивания более высокой орбитали связывающим образом. И, наоборот, если у орбитали превоначально более высокая энергия, то она изменяется путем подмешивания более низкой орбитали антисвязывающим путем. Смешивание выражено тем лучше, чем больше перекрывание, и тем меньше, чем больше начальная разница в энергиях взаимодействующих орбиталей.
Возмущение первого порядка
Когда орбитали обладают одинаковой энергие (вырожденные орбитали), $a_d=a_a=a$, поэтому
Допуская, что $a,\beta $ -- величины отрицательные, получаем соотношения
где $E_+$- энергия нижней возмущенной орбитали $\psi $+;
где $E_-$ - энергия верхней возмущенной орбитали $\psi $-.
Интеграл перекрывания всегда положительная величина, $\left(1+S\right) >\left(1-S\right).$ Нижняя возмущенная орбиталь менее связывает донор и акцептор, чем возмущенная орбиталь эту связь разрыхляет.
Довольно часто применяют упрощение, которое заключается в пренебрежении интегралом перекрывания, допуская, что $S=0$:
В этом случае асимметрия расщепления уровней пропадает.
Волновые функции $\psi $+ и $\psi $- равны:
где $C$ и $C^*$ - коэффициенты, с которыми орбитали $\psi_d$ и $\psi_a$ входят в орбитали $\psi $+ и $\psi $-.
Для возмущения первого порядка все коэффициенты одинаковы
Согласно условию нормировки для каждой орбитали $\sum{C^2}=1$.
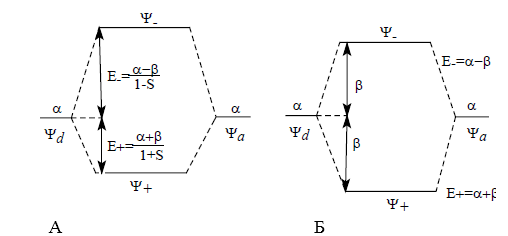
Рисунок 3. Возмущение орбиталей первого порядка с учетом перекрывания (А) и без учета перекрывания (Б)
Возмущение второго порядка
Если взаимодействие орбиталей $\psi_d$ и $\psi_a$ сильно отличается по энергии, то говорят о возмущении второго порядка.
В двух новых возмущенных орбиталях коэффициенты $C_d$ и $C_a$ будут сильно отличаться:
Для возмущения второго порядка $C_d\gg C_a$ и $C^*_a\gg C^*_d$. «Смешиваются» орбитали не в равных пропорциях. Одна из орбиталей «подмешивается» к другой. Так, при формировании ${\psi }_+$ орбиталь ${\psi }_a$ подмешивается к орбитали ${\psi }_d$, а при формировании ${\psi }_-$, наоборот, орбиталь ${\psi }_d$ подмешивается к ${\psi }_a$.
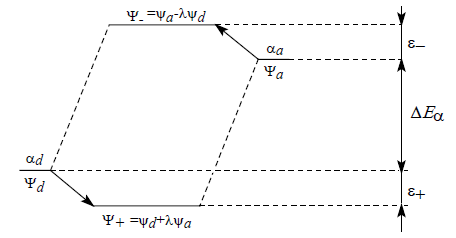
Рисунок 4. Возмущение второго порядка
При введении $\lambda $ - коэффициента «подмешивания» одной базисной орбитали в другую $(0 \[{\psi }_+={\psi }_d+\lambda {\psi }_a,\] \[{\psi }_-={\psi }_a-{\lambda \psi }_d.\]












