Пары орбиталей в альтернантных углеводородах
В альтернантных углеводородах связующие и разрыхляющие МО образуют пары, например для каждой связующей МО с энергией $-E$ имеется разрыхляющая МО с энергией $+E$ (рисунок 1).
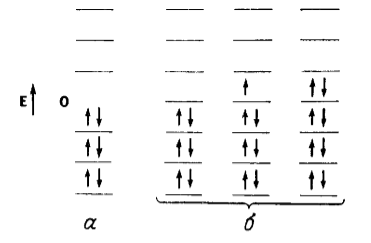 Энергетические уровни четно альтернаитных (а) и нечетно альтернантных (б) углеводородов. Стрелки обозначают электроны. Показаны МО с различными энергиями но некоторые могут быть вырожденными">
Энергетические уровни четно альтернаитных (а) и нечетно альтернантных (б) углеводородов. Стрелки обозначают электроны. Показаны МО с различными энергиями но некоторые могут быть вырожденными">
Рисунок 1. Энергетические уровни четно альтернаитных (а) и нечетно альтернантных (б) углеводородов. Стрелки обозначают электроны. Показаны МО с различными энергиями но некоторые могут быть вырожденными
Четноальтернантными называют углеводороды с четным количеством сопряженных атомов, они имеют равное число отмеченных звездочкой и неотмеченных атомов. В четно альтернантных углеводородах все связывающие орбитали заполненны, а все $\pi $-электроны одинаково распределяються между атомами с ненасыщенными связями.
Нечетноальтернантные углеводороды, как и системы алкенов, помимо равного количества противоположных по энергии связующих и разрыхляющих орбиталей имеют еще несвязующую орбиталь с нулевой энергией $E=0$.
К таким системам можно отнести системы карбокатионов, карбанионов, свободных радикалов. При перекрывании нечетных количеств орбиталей образуются нечетные количества новых МО. Поскольку в альтернантных углеводородах МО существуют парами, с $+E$ и $-E$ -энергией, у одной орбитали, которая не имеет партнера, должна быть нулевая энергия ($E=0$) связывания (рисунок 2).
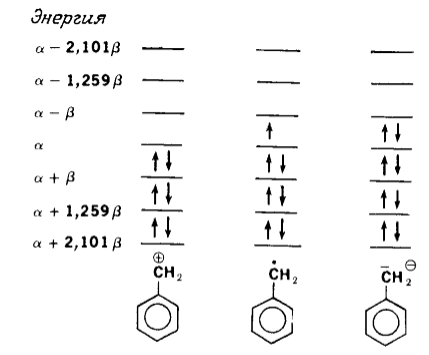
Рисунок 2. Энергетические уровни нечетноальтернантных углеводородов (для примера взята бензильная система). Так как а энергия $\pi $-МО, несвязующая орбиталь имеет нулевую энергию
Построения $\pi$-систем парных орбиталей альтернантных углеводородов
При построениях $\pi$-систем алкенов из двух локализованных $\pi$-связей расположение МО остается симметричным относительно энергетического уровня р- атомной орбитали (рисунок 3).
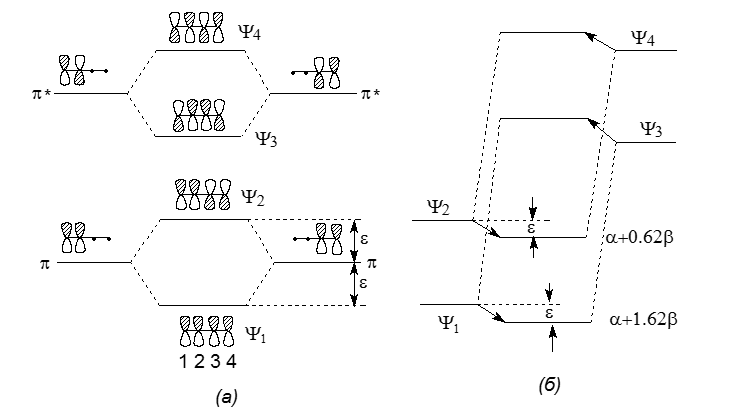
Рисунок 3. (а) Возмущение первого порядка орбиталей в алкенах при образовании ненасыщенной $\pi$-системы. (б) Возмущение второго порядка
Такую же картину можно наблюдать при соединении двух бутадиеновых фрагментов в октатетраен или при соединении бутадиеновых фрагментов двумя концами с этиленовыми фрагментами в молекулы бензола. В таких этих случаях начинют с двух симметричных наборов МО, и в результате возмущений получют также симметричные орбитали конечного полиена. Каждой связующей МО с энергией ($\alpha$-$\epsilon$) соответствует парная МО с энергией ($\alpha$+$\epsilon$), где $\alpha$ это энергия одиночной $p$- орбитали.
Для $\pi$-систем с нечетными количествами атомов углерода МО соответственно тоже нечетное количество. При этом одна орбиталь (средняя) является несвязующей, но общая картина все равно остается симметричной. Это значит, что каждой связывающей орбитали соответствует парная антисвязующая орбиталь (рисунок 4).
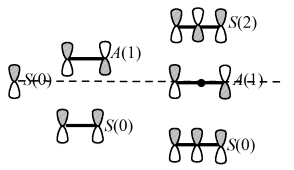
Рисунок 4. Симметрия и узловые свойства $\pi$-МО линейных полиненасыщенных систем . Орбитали симметричны ($S$) или антисимметричны ($A$) относительно центральной зеркальной плоскости
Парность МО является характерным свойством любых альтернантных углеводородов.
Теорема парности относительно квантовой теории строения молекул
Как уже было сказано: теорема парности утверждает, что в любом альтернантном углеводороде все молекулярные орбитали разбиваются на симметричные относительно нулевого уровня ($x=0$) пары. То есть каждой связывающей молекулярной орбитали с энергией $- x$, (в единицах $\frac{\alpha -Е}{\beta}$ соответствует антисвязующая с энергией $x$. Следствия этого положения подтверждены расчетами, представленными графически на рисунках 5 и 6.
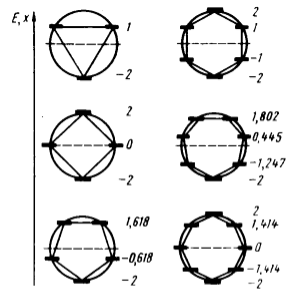
Рисунок 5. Графическое определение энергетических уровней аннуленов в единицах $\frac{\alpha -Е}{\beta}$
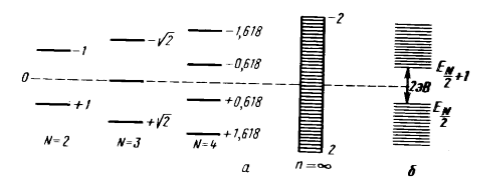 уровней энергии от длины ($N$ - четное число): а --- расчет МОХ; б --- эксперимент">
уровней энергии от длины ($N$ - четное число): а --- расчет МОХ; б --- эксперимент">
Рисунок 6. Зависимость молекулярных уровней энергии от длины ($N$ - четное число): а --- расчет МОХ; б --- эксперимент
Между коэффициентами при АО в таких связывающих (индекс $і$) и антисвязующих (индекс $j$) МО также существует простое соотношение: коэффициенты в антисвязывающих МО на атомах со звездочкой совпадают по значению и знаку с коэффициентами АО атомов со звездочкой в связывающих МО, а на атомах без звездочки меняют знак на обратный:
$x_i = -x_j$
$C{\mu i}^* = C_{\mu j}$
$C_{vi} = -C_{vj}$
Примером, показывающим справедливость этого вывода, могут служить молекулярные орбитали аллила и бутадиена.












