Понятие операция симметрии
Если над объектом произведено действие, приведшее к новой ориентации объекта, неотличимой и совмещаемой с исходной, то такое действие называют операцией симметрии.
Операции симметрии производят такое действие, при котором достаточным условием является неподвижность одной точки объекта. В этом случае говорят о точечных операциях, а неподвижная точка объекта является его центром тяжести, в котором пересекаются все оси и плоскости симметрии.
Неподвижная точка объекта находится либо в центре шара, либо в центре тетраэдра. Каждой операции симметрии подходит определенный элемент симметрии.
Элемент симметрии – это геометрическое место точек, которые остаются неподвижными при данной операции симметрии.
Основные элементы симметрии:
- собственные оси вращения $C_n$, где $n$ – порядок оси, показывающий, что поворот молекулы на угол $2\pi/n$ приводит к структуре, тождественной первоначальной;
- несобственные оси вращения (зеркально – поворотные) $S_n$;
- зеркальные плоскости симметрии $\sigma$, делят молекулу на две равные части таким образом, что одна половина молекулы является зеркально – симметричной другой;
- центр инверсии $i$;
- тождественное преобразование $E$.
Среди операций симметрии различают:
- поворот вокруг оси симметрии $C_n$;
- поворот вокруг оси с вытекающим отражением в плоскости, ортогональной этой оси $S_n$;
- отражение в плоскости симметрии $\sigma$;
- инверсия в центре симметрии $i$;
- операция идентичности $E$.
Операция идентичности позволяет внести в общую классификацию и симметричные и несимметричные объекты.
Собственная ось симметрии
Любая молекула имеет элементарную ось $C_1$, вращение молекулы на 360º возвращает ее в исходное положение. Таким образом, операция $C_1$ равноценна операции идентичности.
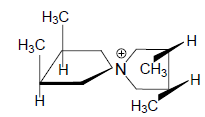
Дихлорметан имеет ось $C_2$, аммиак – ось $C_3$, метан располагает четырьмя осями $C_3$, тетрахлорплатинат имеет ось $C_4$.

Несобственная ось симметрии
Простейшая зеркально – поворотная ось $S_1$ идентична ортогональной ей плоскости симметрии $S_1=\sigma.$
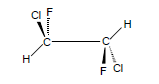
Зеркально – поворотные оси хлорфторметана более высокого порядка можно расценивать как сочетание вращения на угол $2\pi/n$ c последующим отражением в плоскости, которая является перпендикулярной оси вращения.
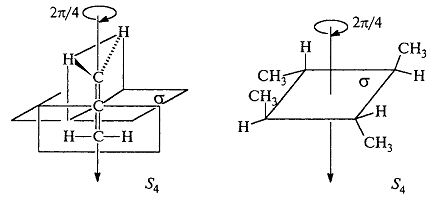
Аллен и изомер 1,2,3,4-тетраметилциклобутан обладают зеркально – поворотной осью $S_4$:
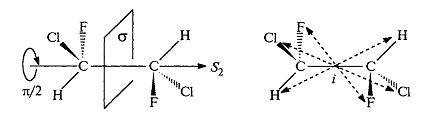
1,2-дихлор-1,2-дифторэтан имеют ось $S_2$, совпадающую со связью $C-C$. Операция $S_2$ идентична инверсии в центре симметрии, который расположен посередине связи $C-C$:
Типы точечных групп симметрии
Так как молекула может иметь несколько элементов симметрии, их удобно систематизировать по точечной группе симметрии. Группу симметрии образует комплекс всех операций симметрии объекта. Если центр тяжести объекта при всех преобразованиях остается неподвижным, то группа симметрии называется точечной.
Типы точечных групп симметрии:
-
Неаксиальные точечные группы, не содержащие нетривиальных поворотных осей ($C_1$, $C_s$, $C_i$).
-
Точечные группы с единственной поворотной осью. Группа $C_n$ элементов симметрии не содержит, группа $C_{nv}$ имеет $n$ вертикальных плоскостей $\sigma n$, которые проходят через ось $C_n$, группа $C_{nh}$ содержит одну горизонтальную плоскость $\sigma h$, перпендикулярную оси $C_n$. Группа $S_n$ при наличии зеркально – поворотной оси порядка $n$ имеет собственную ось порядка $n/2$. При нечетном $n$ оси $S_n$ могут быть представлены как совокупность других операций. Для низших порядков $S_1=\sigma$, $S_2=i$.
-
Диэдральные точечные группы имеют одну ось $C_n$ и $n$ осей второго порядка, ортогональных оси $C_n$. Если плоскости симметрии отсутствуют, группа обозначается $D_n$, при наличии нескольких вертикальных плоскостей симметрии $\sigma_v – D_{nd}$, при наличии горизонтальной плоскости $\sigma_h – D_{nh}$.
-
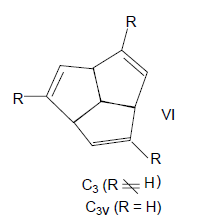
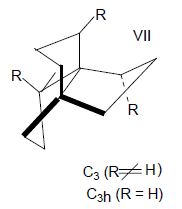
Кубические точечные группы имеют более одной оси порядка выше двух. Это точечные группы правильных тетраэдра ($T_d$), октаэдра и куба ($O_h$), икосаэдра и додекаэдра ($I_h$).Предельной группе $K_h$ принадлежит шар, имеющий максимальную симметрию и вклчающий все возможные операции симметрии.
Понятия «тетраэдрическое строение» и «симмертия $T_d$» не тождественны.
Молекула хлороформа имеет тетраэдрическое строение, но ее симметрия принадлежит к группе $C_{3v}$, а не к группе $T_d$.