Метод Хюккеля

Известно, что для определения $MO$ и соответствующих значений энергии по методу молекулярных орбиталей ($MMO$), необходимо решать вековое уравнение:

$\left|H_{\mu \, v} -ES_{\mu \, v} \right|=0$ (1)

Согласно этому методу, волновая функция, т.е.молекулярная орбиталь

($MO$) ищется в виде линейной комбинации атомных орбиталей-ЛКАО:

$\psi =\sum \limits _{\mu } c_{\mu } \varphi _{\mu } $ (2)

$\varphi _{\mu } $- $AO$, $\psi $ - $MO$.

Хюккель предложил простую форму метода молекулярных орбиталей ($MMO$), которая дала возможность значительно упростить детерминант (1). Сущность этого упрощения заключается в том, что $\pi $ и $\sigma $ -связи разделяются и рассматриваются только $\pi $ -связи. Сделано 2 допущения:

1. Все $\pi $ -орбитали имеют одну узловую плоскость.

2. Длина всех связей одинакова. Рассматриваются только соседние атомы, т.е. пренебрегается всеми несоседними взаимодействиями.

Принятые упрощения можно считать справедливыми только для ненасыщенных углеводородов. Рассматривается линейная комбинация $2p_{z} $ $AO$ атома углерода, образующих нелокализованные $\pi $- связи. Атомы водорода в этом методе не рассматриваются.

Приближения в методе Хюккеля

Метод Хюккеля допускает следующие приближения:

1. Интегралы перекрывания для $AO$, относящихся к соседним атомам, считаются равными нулю:

   \[S_{\mu \, v} =\left\{\begin{array}{l} {1\, \, \, \mu =v} \\ {0\, \, \, \mu \ne v} \end{array}\right. \, \, \, \, \, S_{\mu \, v} =\int \varphi _{\mu } \varphi _{v} dV \]

2. Интегралы $H_{\mu \, v} $ полагаются одинаковыми для всех атомов. Их обозначают буквой $\alpha $ и называют кулоновским интегралом:

   \[\, \, \, \, H_{\mu \, \mu } =\int \varphi _{\mu } \hat{H}\varphi _{\mu } dV =\alpha ,\, \, \, \, \, \alpha \, Эти интегралы характеризуют энергию электронов $2p_{z} $ $AO$ углерода.

   Значение $\alpha $ обычно принимается равным потенциалу ионизации атомов углерода (с обратным знаком) в $2p$ валентном состоянии.

3. Интегралы $H_{\mu \, v} $ принимаются одинаковыми для всех пар, непосредственно связанных между собой, с номерами $\mu $ и $v$ (т.е. соседние атомы: $\mu \to v$).

   Их обозначают буквой $\beta $ и наз. резонансным интегралом:

   \[\, \, \, \, H_{\mu \nu \, } =\int \varphi _{\mu } \hat{H}\varphi _{\nu } dV =\beta ,\, \, \, \, \beta \, Резонансный интеграл -- это отрицательная величина, равная энергии заряда, распределенного с плотностью $\varphi _{\mu } \varphi _{v} $ в поле ядер, экранированных $\sigma $-электронами. Резонансный интеграл характеризует энергию взаимодействия между двумя атомными орбиталями.

4. Интеграл $\, \, \, \, H_{\mu \, v} =0$ для всех атомов, непосредственно не связанных между собой. Величинами $\alpha $ и $\beta $ пользуются как параметрами при расчетах. При этих предположениях уравнение:

   \[\sum \limits _{v} \left(H_{\mu \, v} -ES_{\mu \, v} \right)\, c_{v} =0\]

   может быть записано:

   $\left. \begin{array}{l} {c_{1} \left(\alpha -E\right)+c_{2} \beta _{12} +...+c_{n} \beta _{1n} =0} \\ {c_{1} \beta _{21} +c_{2} \left(\alpha -E\right)+...+c_{n} \beta _{2n} =0} \\ {..............................................} \\ {c_{1} \beta _{n1} +c_{2} \beta _{n2} +...+c_{n} \left(\alpha -E\right)=0} \end{array}\right\}$ (4)

   Эта система уравнений имеет решения, отличные от 0, если ее детерминант равен нулю, т.е.

   $\left|\begin{array}{l} {} \\ {} \\ {} \\ {} \end{array}\right. \begin{array}{cccc} {\left(\alpha -E\right)} & {\beta _{12} ....} & {} & {\beta _{1n} } \\ {\beta _{21} } & {\left(\alpha -E\right)} & {} & {\beta _{2n} } \\ {......} & {.....} & {} & {.....} \\ {\beta _{n1} } & {\beta _{n2} } & {} & {\left(\alpha -E\right)} \end{array}\left. \begin{array}{l} {} \\ {} \\ {} \\ {} \end{array}\right|=0$ (5)

   Систему уравнения (4) можно записать в более упрощенном виде, если ввести следующие обозначения:

   $c_{\mu } \left(\alpha -E\right)+\sum \limits _{\mu \to v} c_{v} \beta =0$ (6)

   $X=\frac{\alpha -E}{\beta } \, \, \, \, Xc_{\mu } +\sum \limits _{\mu \to v} c_{v} =0$ (7)

   Решая уравнения, полученные при раскрытии детерминанта (5), получим $n$ значений для энергии, выше и ниже нулевого значения.

   $E_{\mu } =\alpha +m_{\mu } \beta $ (8)

   \[\mu =1,...,n\]

   За нуль энергии принимается значение величины $\alpha $, т.е. энергия электрона на $2p_{z} $ $AO$ изолированного атома углерода. Графически это изображается в следующем виде:

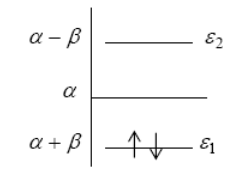
Рисунок 1.

Расчет молекулы этилена ($C_{2} H_{4} $)

Рассмотрим применение метода Хюккеля к молекуле этилена $C_{2} H_{4}$.

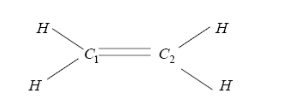
Рисунок 2.

Обозначим $\pi $ -электроны $C_{2} H_{4} $ цифрами $1$ и $2$

Согласно формуле (6) напишем систему уравнений и вычислим

детерминант:

Коэффициенты «С» определим из условия нормировки:

$c_{1}^{2} =\frac{1}{2} $; $c_{1} =\pm \sqrt{\frac{1}{2} } =\pm \frac{1}{\sqrt{2} } $ . Так как выбор знака коэффициента произволен, то принимаем $c_{1} =\frac{1}{\sqrt{2} } $

Тогда:

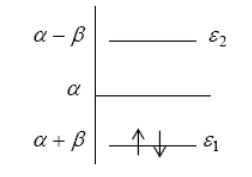
Рисунок 3.

Функция $\psi _{1} $ характеризуется более низкой энергией электрона, чем в изолированном атоме углерода ( величина $\alpha $ в приближении Хюккеля ) и поэтому она является связывающей молекулярной орбиталью;

$\psi _{2} $- разрыхляющая орбиталь, так как ей соответствует более высокая , чем в изолированном атоме , энергия электрона. Согласно принципу Паули, два

$\pi $- электрона молекулы этилена находятся на уровне E1 c противоположными

спинами. Общее значение энергии этих электронов $\, \, \, E_{\pi } =2(\alpha +\beta )$.