Угол между векторами
Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.
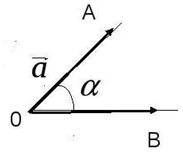
Пусть нам даны два вектора $\overline{α}$ и $\overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $\overline{α}=\overline{OA}$ и $\overline{β}=\overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).
Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ
Причем мы будем считать, что если векторы $\overline{α}$ и $\overline{β}$ будут сонаправленными, или один или оба из них нулевой, то угол между этими векторами будет равен $0^\circ$.
Обозначение: $∠(\overline{α},\overline{β})$
Понятие векторного произведения векторов и формула нахождения
Векторным произведением двух векторов называется вектор, перпендикулярный обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $\overline{α}х\overline{β}$.
Математически это выглядит следующим образом:
- $|\overline{α}х\overline{β}|=|\overline{α}||\overline{β}|sin∠(\overline{α},\overline{β})$
- $\overline{α}х\overline{β}⊥\overline{α}$, $\overline{α}х\overline{β}⊥\overline{β}$
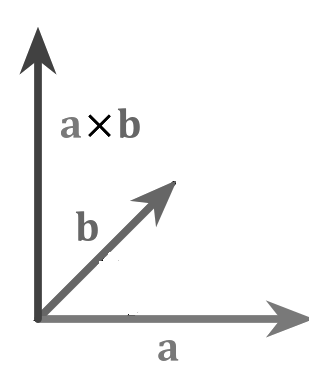
- $(\overline{α}х\overline{β},\overline{α},\overline{β})$ и $(\overline{i},\overline{j},\overline{k})$ одинаково ориентированы (рис. 2)
Рисунок 2. Произведение векторов. Автор24 — интернет-биржа студенческих работ
Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:
- Если длина одного или обоих векторов равняется нулю.
- Если угол между этими векторами будет равняться $180^\circ$ или $0^\circ$ (так как в этом случае синус равняется нулю).
Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решения.
Найти длину вектора $\overline{δ}$, который будет являться результатом векторного произведения векторов, с координатами $\overline{α}=(0,4,0)$ и $\overline{β}=(3,0,0)$.
Решение.
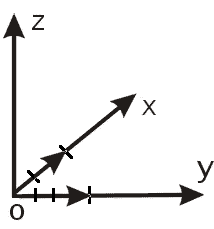
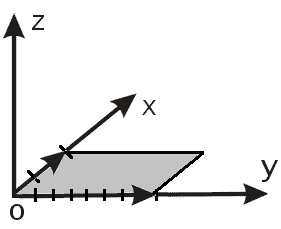
Изобразим эти векторы в декартовом координатном пространстве (рис. 3):
Рисунок 3. Векторы в декартовом координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^\circ$. Найдем длины этих векторов:
$|\overline{α}|=\sqrt{0+16+0}=4$
$|\overline{β}|=\sqrt{9+0+0}=3$
Тогда, по определению 1, получим модуль $|\overline{δ}|$
$|\overline{δ}|=|\overline{α}||\overline{β}|sin90^\circ=4\cdot 3\cdot 1=12$
Ответ: $12$.
Вычисление векторного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}$
Иначе, раскрывая определитель, получим следующие координаты
$\overline{α}х\overline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$
Найти вектор векторного произведения коллинеарных векторов $\overline{α}$ и $\overline{β}$ с координатами $(0,3,3)$ и $(-1,2,6)$.
Решение.
Воспользуемся формулой, приведенной выше. Получим
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\0&3&3\\-1&2&6\end{vmatrix}=(18-6)\overline{i}-(0+3)\overline{j}+(0+3)\overline{k}=12\overline{i}-3\overline{j}+3\overline{k}=(12,-3,3)$
Ответ: $(12,-3,3)$.
Свойства векторного произведения векторов
Для произвольных смешанных трех векторов $\overline{α}$, $\overline{β}$ и $\overline{γ}$, а также $r∈R$ справедливы следующие свойства:
$\overline{α}х\overline{β}=-(\overline{β}х\overline{α})$
Верность этого свойства будет следовать из третьего пункта определения 1.
$(r\overline{α})х\overline{β}=r(\overline{α}х\overline{β})$ и $\overline{α}х(r\overline{β})=r(\overline{α}х\overline{β})$
Из формулы для нахождения векторного произведения будем получать:
$(r\overline{α})\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\rα_1&rα_2&rα_3\\β_1&β_2&β_3\end{vmatrix}=r\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}=r(\overline{α}х\overline{β})$
$\overline{α}х(r\overline{β})=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\rβ_1&rβ_2&rβ_3\end{vmatrix}=r\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}=r(\overline{α}х\overline{β})$
$\overline{α}х(\overline{β}+\overline{γ})=\overline{α}\overline{β}+\overline{α}\overline{γ}$ и $(\overline{α}+\overline{β})\overline{γ}=\overline{α}\overline{γ}+\overline{β}\overline{γ}$.
Данное свойство векторного произведения векторов также можно проверить с помощью формулы.
Следующее свойство называют геометрическим смыслом векторного произведения:
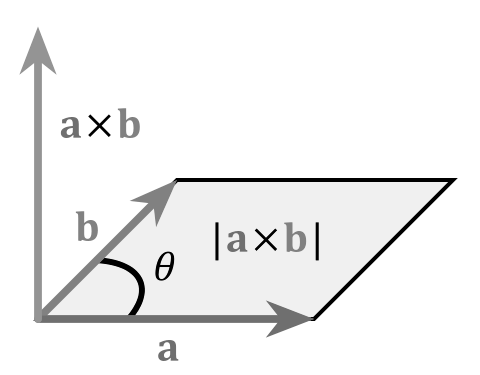
Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)
Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ
Найдите площадь параллелограмма, вершины которого имеют координаты $(3,0,0)$, $(0,0,0)$, $(0,8,0)$ и $(3,8,0)$.
Решение.
Вначале изобразим данный параллелограмм в координатном пространстве (рис.5):
Рисунок 5. Параллелограмм в координатном пространстве. Автор24 — интернет-биржа студенческих работ
Видим, что две стороны этого параллелограмма построены с помощью коллинеарных векторов с координатами $\overline{α}=(3,0,0)$ и $\overline{β}=(0,8,0)$. Используя четвертое свойство, получим:
$S=|\overline{α}х\overline{β}|$
Найдем вектор $\overline{α}х\overline{β}$:
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\3&0&0\\0&8&0\end{vmatrix}=0\overline{i}-0\overline{j}+24\overline{k}=(0,0,24)$
Следовательно
$S=|\overline{α}х\overline{β}|=\sqrt{0+0+24^2}=24$
Ответ: $24$.