Понятие коллинеарности векторов
Чтобы понять, что значит коллинеарные векторы, сперва надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.
Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.
Концами отрезка будем называть точки, которые его ограничивают.
Для введения определения вектора один из концов отрезка назовем его началом.
Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.
Обозначение: $\overline{AB}$ - вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.
Иначе одной маленькой буквой: $\overline{a}$ (рис. 1).
Рисунок 1. Обозначение векторов. Автор24 — интернет-биржа студенческих работ
Нулевым вектором будем называть любую точку, которая принадлежит плоскости.
Обозначение: $\overline{0}$.
Далее рассмотрим, какие векторы называются коллинеарными.
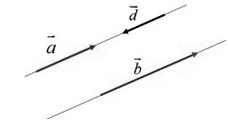
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой. Кроме того, понятие коллинеарность наблюдается в случается параллельности векторов (рис.2).
Рисунок 2. Коллинеарность векторов. Автор24 — интернет-биржа студенческих работ
Также введем определение векторного произведения, которое будет нам необходимо далее.
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.
Обозначение: $\overline{α}х\overline{β}$.
Чтобы найти векторное произведение, будем пользоваться формулой
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}$
Признак коллинеарности через пропорциональность или как определить коллинеарность векторов по координатам
Главное условие коллинеарности векторов: чтобы ненулевые векторы были коллинеарны между собой, необходимо, чтобы их соответствующие координаты были пропорциональны друг другу.
Доказательство.
Необходимость: Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать следующие равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Так как векторы $\overline{α}$ и $\overline{β}$ коллинеарны, то они будут либо сонаправленными, либо противоположно направленными. Без ограничения общности, будем считать, что они будут сонаправлены, то есть $\overline{α}↑↑\overline{β}$. Умножим один из этих векторов на действительное, большее нуля, число $r$, так, чтобы длины векторов $r\overline{α}$ и $\overline{β}$ были равны между собой. По определению умножения векторов на число, получим, что $r\overline{α}↑↑\overline{β}$. Но тогда, по определению равенства векторов, получим, что $r\overline{α}=\overline{β}$. Из этого равенства получим, что
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Достаточность: Пусть верны равенства $α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$. Докажем, что векторы $\overline{α}$ и $\overline{β}$ будут коллинеарными.
Из данных равенств следует, что $r\overline{α}=\overline{β}$.
Имеются два случая:
$r \lt 0$
В этом случае, по определению умножения вектора на число, получим, что $r\overline{α}↑↓\overline{β}$.
$r >0$
В этом случае получим, что $r\overline{α}↑↑\overline{β}$.
Тогда, в обоих случаях получаем доказательство коллинеарности векторов $\overline{α}$ и $\overline{β}$.
Ответ: теорема доказана.
Как проверить коллинеарность векторов $(3,-1)$ и $(9,-3)$.
Доказательство.
Разложим второй вектор:
$(9,-3)=(3\cdot 3,3\cdot (-1) )=3(3,-1)$
Получаем, что координаты этих векторов пропорциональны друг другу, что, по теореме 1, и доказывает наше утверждение.
Признаки и свойства коллинеарности векторов через их произведение
Чтобы ненулевые векторы были коллинеарны между собой, необходимо и достаточно, чтобы их векторное произведение было равно нулевому вектору.
Доказательство.
Необходимость: Пусть нам даны векторы $\overline{α}$ и $\overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они коллинеарны друг другу. Тогда нам нужно доказать, что $\overline{α}х\overline{β}=\overline{0}$.
Так как векторы коллинеарны, то, по теореме 1, верны равенства
$α_1=rβ_1$, $α_2=rβ_2$, $α_3=rβ_3$
Найдем $\overline{α}х\overline{β}$ по формуле
$\overline{α}х\overline{β}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\α_1&α_2&α_3\\β_1&β_2&β_3\end{vmatrix}=\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\rβ_1&rβ_2&rβ_3\\β_1&β_2&β_3\end{vmatrix}=r\begin{vmatrix}\overline{i}&\overline{j}&\overline{k}\\β_1&β_2&β_3\\β_1&β_2&β_3\end{vmatrix}=r\cdot \overline{0}=\overline{0}$
Достаточность: Пусть верно равенство $\overline{α}х\overline{β}=\overline{0}$, докажем, что векторы $\overline{α}$ и $\overline{β}$ коллинеарны. Так как векторное произведение равняется $\overline{0}$, то его длина также равняется нулю. Следовательно, угол между $\overline{α}$ и $\overline{β}$ равняется $180^\circ$ или $0^\circ$. То есть, чтобы они были коллинеарны, векторы должны лежать на одной или параллельных прямых.
Теорема доказана.