Понятие площади
Понятие площади любой геометрической фигуры, в частности треугольника, будем связывать с такой фигурой, как квадрат. За единицу площади любой геометрической фигуры будем принимать площадь квадрата, сторона которого равняется единице. Для полноты, вспомним два основных свойства для понятия площадей геометрических фигур.
Свойство 1: Если геометрические фигуры равны, то значения их площадей также равны.
Свойство 2: Любая фигура может быть разбита на несколько фигур. Причем площадь первоначальной фигуры равняется сумме значений площадей всех составляющих её фигур.
Рассмотрим пример.
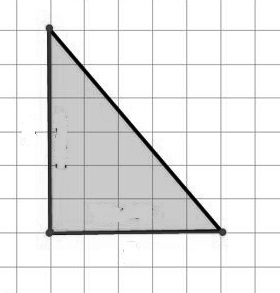
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Решение.
Очевидно, что одна из сторон треугольника является диагональю прямоугольника, у которого одна сторона имеет длину $5$ (так как $5$ клеток), а вторая $6$ (так как $6$ клеток). Следовательно, площадь этого треугольника будет равняться половине такого прямоугольника. Площадь прямоугольника равняется
$5\cdot 6=30$
Тогда площадь треугольника равняется
$30:2=15$
Ответ: $15$.
Далее рассмотрим несколько методов для нахождения площадей треугольников, а именно с помощью высоты и основания, с помощью формулы Герона и площадь равностороннего треугольника.
Как найти площадь треугольника через высоту и основание
Площадь треугольника можно найти как половину произведения длины стороны, на высоту, проведенную к этой стороне.
Математически это выглядит следующим образом
$S=\frac{1}{2}αh$
где $a$ - длина стороны, $h$ - высота, проведенная к ней.
Доказательство.
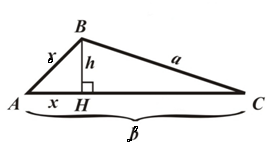
Рассмотрим треугольник $ABC$, в котором $AC=α$. К этой стороне проведена высота $BH$, которая равняется $h$. Достроим его до квадрата $AXYC$ как на рисунке 2.
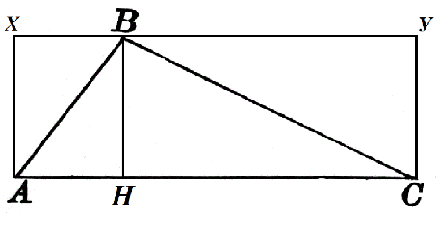
Площадь прямоугольника $AXBH$ равняется $h\cdot AH$, а прямоугольника $HBYC$ равняется $h\cdot HC$. Тогда
$S_ABH=\frac{1}{2}h\cdot AH$, $S_CBH=\frac{1}{2}h\cdot HC$
Следовательно, искомая площадь треугольника, по свойству 2, равняется
$S=S_ABH+S_CBH=\frac{1}{2}h\cdot AH+\frac{1}{2}h\cdot HC=\frac{1}{2}h\cdot (AH+HC)=\frac{1}{2}αh$
Теорема доказана.
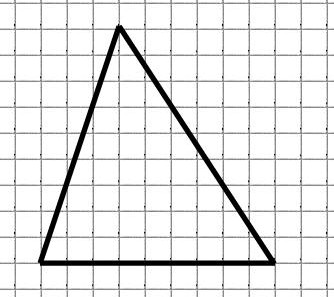
Найти площадь треугольника на рисунке ниже, если клетка имеет площадь, равную единице
Решение.
Основание этого треугольника равняется $9$ (так как $9$ составляет $9$ клеток). Высота также равняется $9$. Тогда, по теореме 1, получим
$S=\frac{1}{2}\cdot 9\cdot 9=40,5$
Ответ: $40,5$.
Формула Герона
Если нам даны три стороны треугольника $α$, $β$ и $γ$, то его площадь можно найти следующим образом
$S=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
здесь $ρ$ означает полупериметр этого треугольника.
Доказательство.
Рассмотрим следующий рисунок:
По теореме Пифагора из треугольника $ABH$ получим
$h^2=γ^2-x^2$
Из треугольника $CBH$, по теореме Пифагора, имеем
$h^2=α^2-(β-x)^2$
$h^2=α^2-β^2+2βx-x^2$
Из этих двух соотношений получаем равенство
$γ^2-x^2=α^2-β^2+2βx-x^2$
То есть
$x=\frac{γ^2-α^2+β^2}{2β}$
Получим
$h^2=γ^2-(\frac{γ^2-α^2+β^2}{2β})^2$
$h^2=\frac{(α^2-(γ-β)^2 )((γ+β)^2-α^2)}{4β^2}$
$h^2=\frac{(α-γ+β)(α+γ-β)(γ+β-α)(γ+β+α)}{4β^2}$
Так как $ρ=\frac{α+β+γ}{2}$, то $α+β+γ=2ρ$, значит
$h^2=\frac{2ρ(2ρ-2γ)(2ρ-2β)(2ρ-2α)}{4β^2}$
$h^2=\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2 }$
$h=\sqrt{\frac{4ρ(ρ-α)(ρ-β)(ρ-γ)}{β^2}}$
$h=\frac{2}{β}\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
По теореме 1, получим
$S=\frac{1}{2} βh=\frac{β}{2}\cdot \frac{2}{β} \sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}=\sqrt{ρ(ρ-α)(ρ-β)(ρ-γ)}$
Теорема доказана.
Площадь равностороннего треугольника
Площадь равностороннего треугольника определяется как произведение квадрата стороны с числом $\frac{\sqrt{3}}{4}$.
Математически это выглядит следующим образом
$S=\frac{α^2\sqrt{3}}{4}$
где $α$ – сторона треугольника.
Доказательство.
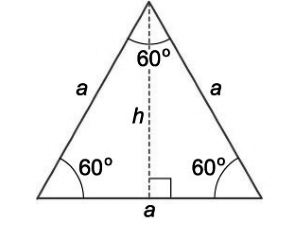
Пусть нам дан равносторонний треугольник, у которого сторона равняется $α$. Проведем высоту $h$ (рис. 5).
Высота равностороннего треугольника является также и медианой, значит, по теореме Пифагора
$h^2=α^2-\frac{α^2}{4}$
$h^2=\frac{3}{4} α^2$
$h=\frac{α\sqrt{3}}{2}$
Значит по теореме 1:
$S=\frac{α^2\sqrt{3}}{4}$
Теорема доказана.
Найти площадь равностороннего треугольника, если его сторона равняется $2$.
Решение.
Используя теорему 3, получим
$S=\frac{4\sqrt{3}}{4}=\sqrt{3}$
Ответ: $\sqrt{3}$.