Сущность координатного метода для решения геометрических задач
Сущностью решения задач с помощью координатного метода состоит в том, чтоб ввести удобную нам в том или ином случае систему координат и переписать все данные с помощью него. После этого все неизвестные величины или доказательства проводятся с помощью этой системы. Как ввести координаты точек в любой системе координат, было нами рассмотрено в другой статье – здесь мы на этом останавливаться не будем.
Введем основные утверждения, которые используются в координатном методе.
Утверждение 1: Координаты вектора будут определяться разностью соответственных координат конца данного вектора и его же начала.
Утверждение 2: Координаты середины отрезка будут определяться как полусумма соответственных координат его границ.
Утверждение 3: Длина любого вектора $\overline{δ}$ с данными координатами $(δ_1,δ_2,δ_3)$ будет определяться формулой
$|\overline{δ}|=\sqrt{δ_1^2+δ_2^2+δ_3^2}$
Утверждение 4: Расстояние между двумя любыми точками, заданными координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$ будет определяться формулой
$d=\sqrt{(δ_1-β_1)^2+(δ_2-β_2)^2+(δ_3-β_3)^2}$
Схема решения геометрических задач с использованием координатного метода
Для решения геометрических задач с помощью координатного метода лучше всего пользоваться данной схемой:
-
Провести анализ того, что дано в задаче:
- Задать наиболее подходящую для задачи систему координат;
- Математически записывается условие задачи, вопрос задачи, строится чертеж по данной задаче.
-
Все данные задачи записать в координатах выбранной системы координат.
- Составить необходимые соотношения из условия задачи, а также связать эти соотношения с тем, что необходимо найти (доказать в задаче).
- Полученный результат перевести на язык геометрии.
Примеры задач, решаемые координатным методом
Основными задачами, приводящими к координатному методу можно выделить следующие задачи (их решения здесь приводить не будем):
- Задачи на нахождение координат вектора по его концу и началу.
- Задачи, связанные с делением отрезка в каком-либо отношении.
- Доказательство того, что три точки лежат на одной прямой или, что четыре точки лежат в одной плоскости.
- Задачи на нахождение расстояния между двумя данными точками.
- Задачи на нахождение объемов и площадей геометрических фигур.
Результаты решения первой и четвертой задачи приведены нами как основные утверждения выше и довольно часто используются для решения других задач с помощью координатного метода.
Примеры задач на применение метода координат
Найти боковую сторону правильной пирамиды, у которого высота равняется $3$ см, если сторона основания равняется $4$ см.
Решение.
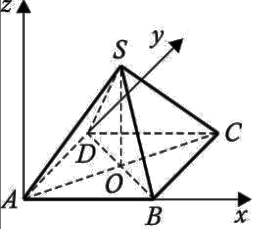
Пусть нам дана правильная пирамида $ABCDS$, высота которой – $SO$. Введем систему координат, как на рисунке 1.
Так как точка $A$ - центр построенной нами системы координат, то
$A=(0,0,0)$
Так как точки $B$ и $D$ принадлежат осям $Ox$ и $Oy$, соответственно, то
$B=(4,0,0)$, $D=(0,4,0)$
Так как точка $C$ принадлежит плоскости $Oxy$, то
$C=(4,4,0)$
Так как пирамида правильная, то $O$ - середина отрезка $[AC]$. По утверждению 2, получаем:
$O=(\frac{0+4}{2},\frac{0+4}{2},\frac{0+0}{2})=(2,2,0)$
Так как высота $SO$ перпендикулярна плоскости $Oxy$, то
$S=(2,2,3)$
По утверждению 4, будем получать
$|AO|=\sqrt{(0-2)^2+(0-2)^2+(0-0)^2}=2\sqrt{2}$
Теперь найдем боковую сторону по теореме Пифагора
$AS^2=9+8$
$AS=\sqrt{17}$
Ответ: $\sqrt{17}$.
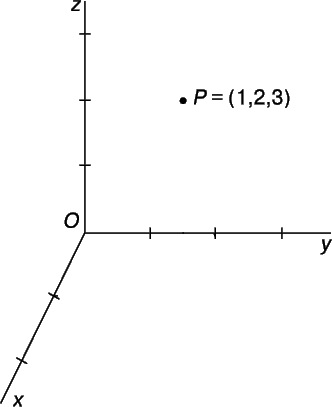
Найти минимальное расстояние от точки $P$ с координатами $(1,2,3)$ до каждой из координатных осей в прямоугольной системе координат (рис. 2)
Решение.
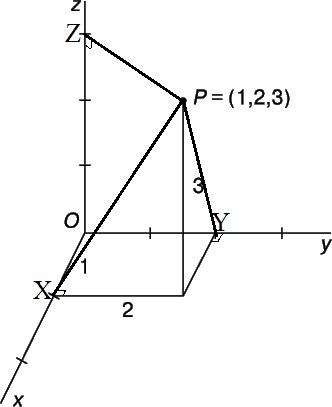
Как нам известно, чтобы найти минимальное расстояние от точки до любой прямой нужно провести к ней перпендикуляр и найти его длину. Проведем перпендикуляры ко всем координатным осям (рис. 3).
Видим, что:
$X=(1,0,0)$, $Y=(0,2,0)$, $Z=(0,0,3)$
Теперь будем находить расстояния по 4 утверждению:
$|PX|=\sqrt{(1-1)^2+(2-0)^2+(3-0)^2}=\sqrt{13}$
$|PY|=\sqrt{(1-0)^2+(2-2)^2+(3-0)^2}=\sqrt{10}$
$|PZ|=\sqrt{(1-0)^2+(2-0)^2+(3-3)^2}=\sqrt{5}$
Ответ: $\sqrt{13}$, $\sqrt{10}$ и $\sqrt{5}$.