Понятие многоугольника
Многоугольником называется геометрическая фигура в плоскости, которая состоит из попарно соединенных между собой отрезков, соседние из которых не лежат на одной прямой.
При этом отрезки называются сторонами многоугольника, а их концы - вершинами многоугольника.
$n$-угольником называется многоугольник, у которого $n$ вершин.
Виды многоугольников
Если многоугольник всегда будет лежать по одну сторону от любой прямой, проходящей через его стороны, то многоугольник называется выпуклым (рис. 1).
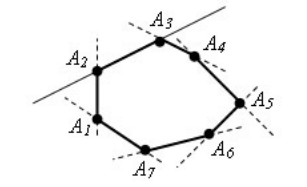
Рисунок 1. Выпуклый многоугольник
Если многоугольник лежит по разные стороны хотя бы одной прямой, проходящей через его стороны, то многоугольник называется невыпуклым (рис. 2).
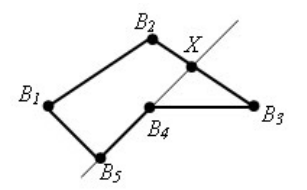
Рисунок 2. Невыпуклый многоугольник
Сумма углов многоугольника
Введем теорему о сумме углов -угольника.
Сумма углов выпуклого -угольника определяется следующим образом
\[(n-2)\cdot {180}^0\]Доказательство.
Пусть нам дан выпуклый многоугольник $A_1A_2A_3A_4A_5\dots A_n$. Соединим его вершину $A_1$ со всеми другими вершинами данного многоугольника (рис. 3).
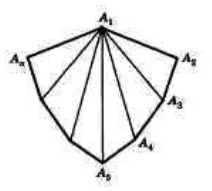
Рисунок 3.
При таком соединении мы получим $n-2$ треугольника. Просуммировав их углы мы получим сумму углов данного -угольника. Так как сумма углов треугольника равняется ${180}^0,$ получим, что сумма углов выпуклого -угольника определяется по формуле
\[(n-2)\cdot {180}^0\]Теорема доказана.
Понятие четырехугольника
Используя определение $2$, легко ввести определение четырехугольника.
Четырехугольником называется многоугольник, у которого $4$ вершины (рис. 4).
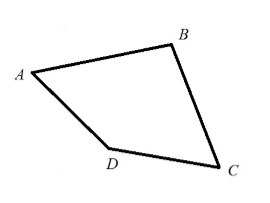
Рисунок 4. Четырехугольник
Для четырехугольника аналогично определены понятия выпуклого четырехугольника и невыпуклого четырехугольника. Классическими примерами выпуклых четырехугольников являются квадрат, прямоугольник, трапеция, ромб, параллелограмм (рис. 5).
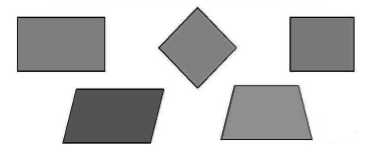
Рисунок 5. Выпуклые четырехугольники
Сумма углов выпуклого четырехугольника равняется ${360}^0$
Доказательство.
По теореме $1$, мы знаем, что сумма углов выпуклого -угольника определяется по формуле
\[(n-2)\cdot {180}^0\]Следовательно, сумма углов выпуклого четырехугольника равняется
\[\left(4-2\right)\cdot {180}^0={360}^0\]Теорема доказана.
Примеры задач
Определить сумму углов выпуклого девятиугольника, семиугольника и двенадцатиугольника.
Решение.
Для решения будем пользоваться теоремой $1$. Получим:
Сумма углов выпуклого пятиугольника равняется
\[\left(5-2\right)\cdot {180}^0=3\cdot {180}^0={540}^0\]Сумма углов выпуклого девятиугольника равняется
\[\left(9-2\right)\cdot {180}^0=7\cdot {180}^0={1260}^0\]Сумма углов выпуклого двенадцатиугольника равняется
\[\left(12-2\right)\cdot {180}^0=10\cdot {180}^0={1800}^0\]Сколько углов имеет выпуклый многоугольник, если сумма его углов равняется ${1620}^0$.
Решение.
Используя формулу задачи $1$, имеем
\[\left(n-2\right)\cdot {180}^0={1620}^0\] \[n-2=9\] \[n=11\]Ответ: $11$.











