Метод комплексных амплитуд
Положение точки на плоскости можно однозначно задать комплексным числом:
Если точка ($А$) вращается, то координаты этой точки изменяются в соответствии с законом:
Используем формулу Эйлера:
запишем $z$ в виде:
где $Re(z)=x$, то есть физическая величина x равна вещественной части комплексного выражения (4). При этом модуль комплексного выражения равен амплитуде колебаний -- $a$, его аргумент равен фазе (${\omega }_0t+\delta $). Иногда при взятии реальной части от $z$ знак операции Re опускают и получают символическое выражение:
Выражение (5) не следует принимать буквально. Часто формально упрощают (5):
где $A=ae^{i \delta}$ -- комплексная амплитуда колебания. Комплексный характер амплитуды $А$ обозначает, что колебание имеет начальную фазу неравную нулю.
Для того чтобы раскрыть физический смысл выражения типа (6), предположим, что частота колебаний (${\omega }_0$) имеет вещественную и мнимую части, и ее можно представить как:
Тогда выражение (6) можно записать как:
В том случае, если ${\omega }2>0,$ то выражение (8) описывает затухающие гармонические колебания с круговой частотой $\omega1$ и показателем затухания ${\omega }_2$. Если ${\omega }_2
Над комплексными величинами можно проводить многие математические операции так, как будто величины являются вещественными. Операции возможны, если они сами линейны и вещественны (такими являются сложение, умножение, дифференцирование по вещественной переменной и другие, но не все). Надо помнить, что комплексные величины сами по себе не соответствуют никаким физическим величинам.
Метод векторных диаграмм
Пусть точка $A$ равномерно вращается по окружности радиуса $r$ (рис.1), скорость ее вращения ${\omega }_0$.

Рисунок 1.
Положение точки $А$ на окружности можно задать с помощью угла $\varphi $. Этот угол равен:
где $\delta =\varphi (t=0)$ величина угла поворота радиус-вектора $\overrightarrow{r}$ в начальный момент времени. Если точка $М$ вращается, то ее проекция на $ось X$ движется по диаметру окружности, совершая гармонические колебания между точками $М$ $N$. Абсциссу точки $А$ можно записать как:
Подобным способом можно представлять колебания любых величин.
Необходимо только принять изображение величины, которая совершает колебания абсциссой точки $А$, которая равномерно вращается по окружности. Можно, конечно использовать и ординату:
Для того чтобы представлять затухающие колебания, надо брать не окружность, а логарифмическую спираль, которая приближается к фокусу. Если скорость приближения движущейся по спирали точки постоянна и очка движется к фокусу, то проекция этой точки на $ось X$ даст формулы затухающих колебаний.
Вместо точки можно использовать радиус-вектор, который будет равномерно вращаться вокруг начала координат. Тогда величина, которая совершает гармонические колебания, будет изображаться как проекция этого вектора на $ось X$. При этом математические операции над величиной $x$ заменяют операциями над вектором.
Так операцию суммирования двух величин:
удобнее заменить суммированием двух векторов (используя правило параллелограмма). Векторы выбрать так, что их проекции на избранную $ось X$ являются выражениями $x_1\ и\ x_2$. Тогда результат операции суммирования векторов в проекции на ось абсцисс будет равен $x_1+\ x_2$.
Продемонстрируем применение метода векторных диаграмм.
Итак, представим комплексные числа векторами на комплексной плоскости. Величина, изменяющаяся по гармоническому закону, изображена вектором, который вращается с частотой ${\omega }0$ вокруг своего начала против часовой стрелки. Длина вектора равна амплитуде колебаний.
Графический метод решения, например, уравнения:
\[IZ=U\ \left(1.1\right),\]где $Z=R+i(\omega L-\frac{1}{\omega C})$ -- импеданс, представим с помощью рис.2. На этом рисунке изображена векторная диаграмма напряжений в цепи переменного тока.
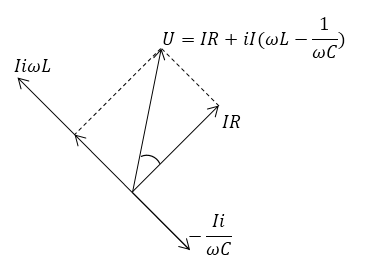
Рисунок 2.
Учтем, что умножение комплексной величины на комплексную единицу означает ее поворот на угол $90^0$ против часовой стрелки, а умножение на ($-i$) на тот же угол по часовой стрелке. Из рис.2 ледует, что:
\[tg\varphi =\frac{\omega L-\frac{1}{\omega C}}{R}\left(1.2\right),\]где $-\frac{\pi }{2}\le \varphi \le \frac{\pi }{2}.$ Изменение угла $\varphi $ зависит от соотношения между импедансами элементов цепи и частотами. Внешнее напряжение может изменяться по фазе, от совпадающего с напряжением на индуктивности, до совпадающего с напряжением на емкости. Выражается это обычно в виде отношения между фазами напряжений на элементах цепи и фазой внешнего напряжения:
-
Фаза напряжения на индуктивности ${(U}L=i\omega LI)$ всегда опережает фазу внешнего напряжения на угол от $0$ до $\pi .$
-
Фаза напряжения на емкости ${(U}C=-\frac{iI}{\omega C}$) всегда отстает от фазы внешнего напряжения на угол между $0$ и --$\ \pi .$
-
При этом фаза на сопротивлении может как опережать, так и отставать от фазы внешнего напряжения на угол между- $\frac{\pi }{2}$ и $\frac{\pi }{2}$.
Векторная диаграмма (рис.2) позволяет сформулировать следующее:
-
Фаза напряжения на индуктивности опережает фазу силы тока на $\frac{\pi }{2}$.
-
Фаза напряжения на емкости отстает на $\frac{\eth }{2}\ $от фазы силы тока.
-
Фаза напряжения на сопротивлении совпадает с фазой силы тока.
Задание: Продемонстрируйте то, что операцию возведения в квадрат нельзя применять к комплексным величинам как к вещественным числам.
Решение:
Допустим, что надо возвести в квадрат вещественное число $x$. Правильный ответ: $x^2$. Формально применим комплексный метод. Произведем замену:
$x\to x+iy$. Возведем полученное выражение в квадрат, получим:
\[{\left(x+iy\right)}^2=x^2-y^2+2xyi\ \left(2.1\right).\]Вещественная часть выражения (2.1) равна:
\[{Re\left(x+iy\right)}^2=Re\left(x^2-y^2+2xyi\right)=x^2-y^2\ne x^2.\]Причина ошибки в том, что операция возведения в квадрат не является линейной.











