Особенности распространения электромагнитной волны в анизотропной среде
Векторы поля плоской волны света можно представить как:
Подставив выражения (1) в уравнения Максвелла, получим формулы:
Волновой вектор $\overrightarrow{k}$ указывает направление распространения фронта волны, то есть, нормален к поверхности одинаковой фазы. Фазовая скорость ($\overrightarrow{v}$) совпадает по направлению с $\overrightarrow{k}$. Направление распространения волны задают вектором $\overrightarrow{n}$, определяемым как:
Из уравнений ($2.c$) и ($2.d$) следует, что волна распространяется перпендикулярно векторам $\overrightarrow{D}\ $и $\overrightarrow{H}.$ Из определения вектора Умова -- Пойнтинга ($\overrightarrow{P}=\overrightarrow{E}\times \overrightarrow{H}$), следует, что поток энергии направлен перпендикулярно векторам $\overrightarrow{E}\ и\ \overrightarrow{H}$. Направление потока энергии в световой волне называют лучом. В общем случае, направление движения волны и направление потока энергии не совпадает. Энергия электромагнитной волны движется с групповой скоростью. Обозначим единичный вектор в направлении луча как:
Тогда можно сказать, что групповая скорость $\overrightarrow{u}$ волны совпадает с направлением $\overrightarrow{\tau }$.
Итак, первой особенностью распространения электромагнитной волны в анизотропной среде является то, что, так как векторы $\overrightarrow{E}$ и $\overrightarrow{D}$ не коллинеарны, направление луча и распространение волны не совпадают (направление групповой и фазовой скорости не совпадают). Уравнение, связывающее векторы $\overrightarrow{E}$ и $\overrightarrow{D}$ можно представить в виде:
Второй особенностью распространения волн света в анизотропной среде является то, что их скорость зависит от направления распространения и поляризации.
Связь фазовой скорости и направления распространения волны
Пусть волна распространяется по оси $Z$, Ось $Z$, в свою очередь, является одной из главных осей тензора диэлектрической проницаемости (${\varepsilon }_{ij}$). Допустим, что вектор $\overrightarrow{D}$ коллинеарен оси $X$ (это значит, что $D_x\ne 0,\ D_y=D_z=0$) и, значит, вектор $\overrightarrow{H}$ коллинеарен оси $Y$. При этом имеем: $E_x=\frac{D_x}{{\varepsilon }_0{\varepsilon }_x},\ E_y=E_z=0.\ $Уравнения (2 a,b) принимают вид:
Перемножим левые части уравнений (6.a) и (6.b) и правые части, получим:
Из выражения (7) следует, что:
Из выражения (8) фазовая скорость равна:
где индекс $x$ у фазовой скорости значит, что это скорость волны, векторы которой $\overrightarrow{E}$ и $\overrightarrow{D}$ коллинеарны оси X. В случае коллинеарности $\overrightarrow{E}$ и $\overrightarrow{D}$ оси $Y$, имеем:
Так как в общем случае ${\varepsilon }_x\ne {\varepsilon }_y$, то делаем вывод о том, что фазовая скорость волны отлична для двух направлений колебаний вектора $\overrightarrow{E}$. Следовательно, в направлении оси $Z$ распространяются только волны, в которых векторы $\overrightarrow{E}$ и $\overrightarrow{D}$ совершают колебания параллельно либо оси $X$, или оси $Y$.
Фазовую скорость можно найти, используя уравнение Френеля:
где $v_i$ -- главные скорости распространения волны (фазовая скорость волны , соответствующая оси $X_i).$ Надо отметить, что она не является проекцией фазовой скорости волны на ось $X_i$, а характеризует фазовую скорость волны векторы $\overrightarrow{E}$ и $\overrightarrow{D}$ в которой коллинеарны данной оси. $v=\frac{\omega }{k},$ $n_i:\ n_1,\ n_2,n_3$ -- направляющие косинусы. Решение уравнения (5) дает фазовую скорость ($v$) как функцию от $n_i\ и\ v_i$.
Фазовую скорость часто выражают как функцию от направления вектора $\overrightarrow{D}.$ Если обозначить единичный вектор $\overrightarrow{d}$, определяемый как:
то выражение для модуля фазовой скорости можно записать как:
что означает, фазовая скорость определяется направлением вектора электрического смещения.
Задание: Пусть вектор $\overrightarrow{n}$ по оси $Z$. Запишите выражения для фазовых скоростей световой волны.
Решение:
Если вектор, определяющий направление распространения волны направлен по оси $Z$, это значит, что его компоненты равны:
\[\overrightarrow{n}=\left(n_x,n_y,\ n_z\right)=\left(0,0,1\right)\left(1.1\right).\]В качестве основы для решения задачи используем векторное уравнение:
\[\overrightarrow{D}=\frac{c^2}{v^2}{\varepsilon }_0\left[\overrightarrow{E}-\overrightarrow{n}\left(\overrightarrow{n}\overrightarrow{E}\right)\right]\left(1.2\right).\]Тогда в проекции на ось $X$ (1.2) запишем как:
\[D_x={\varepsilon }_0{\varepsilon }_xE_x=\frac{c^2}{v^2}{\varepsilon }_0\left[E_x-n_x\left(\overrightarrow{n}\overrightarrow{E}\right)\right]=\frac{c^2}{v^2}{\varepsilon }_0E_x\left(1.3\right).\]В таком случае имеем:
\[v_1=\frac{c}{\sqrt{{\varepsilon }_x}}=v_x.\]В проекции на ось $Y$ уравнение (1.2) представим как:
\[D_y={\varepsilon }_0{\varepsilon }_yE_y=\frac{c^2}{v^2}{\varepsilon }_0\left[E_y-n_y\left(\overrightarrow{n}\overrightarrow{E}\right)\right]=\frac{c^2}{v^2}{\varepsilon }_0E_y\left(1.4\right).\] \[v_2=\frac{c}{\sqrt{{\varepsilon }_y}}=v_y.\]В проекции на ось $Z$:
\[D_z={\varepsilon }_0{\varepsilon }_zE_z=\frac{c^2}{v^2}{\varepsilon }_0\left[E_z-n_z\left(\overrightarrow{n}\overrightarrow{E}\right)\right]=\frac{c^2}{v^2}{\varepsilon }_0{(E}_z-E_z)=0(1.5).\] \[v_z=0.\]Ответ: Две волны со скоростями: $v_x=\frac{c}{\sqrt{{\varepsilon }_x}},\ v_y=\frac{c}{\sqrt{{\varepsilon }_y}}.$ Это скорости волн, котрые поляризованы в направлениях $X$ и $Y$.
Задание: Изобразите взаимное расположение векторов плоской световой волны в анизотропной среде.
Решение:
Рассмотрим уравнения:
\[-\overrightarrow{k}\times \overrightarrow{H}=\omega \overrightarrow{D};\ \overrightarrow{\ k}\times \overrightarrow{E}=\omega {\mu }_0\overrightarrow{H};\overrightarrow{k}\overrightarrow{D}=0;\ \overrightarrow{k}\overrightarrow{H}=0(2.1).\ \]и определения векторов:
\[\overrightarrow{n}=\frac{\overrightarrow{k}}{k},\overrightarrow{\tau }=\frac{\overrightarrow{P}}{P}\ и\ \overrightarrow{P}=\overrightarrow{E}\times \overrightarrow{H}\ \left(2.2\right).\]Очевидно, что $\overrightarrow{n}\bot \overrightarrow{H,\ }$ $\overrightarrow{\tau }\bot \overrightarrow{H}$. При этом $\overrightarrow{E}\bot \overrightarrow{H,\ }\ \overrightarrow{D}\bot \overrightarrow{H\ .}\ \overrightarrow{n}\bot \overrightarrow{D,\ }$ $\overrightarrow{\tau }\bot \overrightarrow{E}$. Значит, векторы $\overrightarrow{E}$, $\overrightarrow{D}$, $\overrightarrow{n}$ и $\overrightarrow{\tau }$ находятся в одной плоскости, перпендикулярной $\overrightarrow{H.}$ Причем угол между векторами $\overrightarrow{n}$ и $\overrightarrow{\tau }$ равен углу между $\overrightarrow{E}$ и $\overrightarrow{D}\ (рис.1).\ $
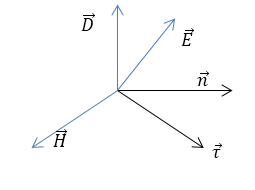
Рисунок 1.













