Что такое Броуновское движение
Броуновским движением называют непрерывное хаотическое движение малых частиц, взвешенных в жидкости или газе.
Это движение характеризуется следующими чертами:
- продолжается неограниченно долго без каких бы то ни было видимых изменений,
- интенсивность движения броуновских частиц зависит от их размеров, но не зависит от их природы,
- интенсивность возрастает с ростом температуры,
- интенсивность возрастает с уменьшением вязкости жидкости или газа.
Броуновское движение не является молекулярным движением, но служит непосредственным доказательством существования молекул и хаотического характера их теплового движения.
Сущность Броуновского движения
Сущность этого движения в следующем. Частица вместе с молекулами жидкости или газа образуют одну статистическую систему. В соответствии с теоремой о равномерном распределении энергии по степени свободы на каждую степень свободы приходится 1/2kT энергии. Энергия 2/3kT, приходящаяся на три поступательные степени свободы частицы, приводит к движению ее центра масс, которое наблюдается под микроскопом в виде дрожания частицы. Если броуновская частица достаточно жесткая, то еще 3/2kT энергии приходится на ее вращательные степени свободы. Поэтому при своем дрожании она испытывает еще и постоянные изменения ориентировки в пространстве.
Можно объяснить броуновское движение и так: причиной Броуновского движения являются флуктуации давления, которое оказывается на поверхность малой частицы со стороны молекул среды. Сила и давление изменяется по модулю и направлению, в результате чего частица находится в беспорядочном движении.
Движение броуновской частицы является случайным процессом. Вероятность (dw) того, что броуновская частица, находившаяся в однородной изотропной среде в начальный момент времени (t=0) в начале координат, сместится вдоль произвольно направленной (при t$>$0) оси Ox так, что ее координата будет лежать в интервале от x до x+dx, равна:
\[dw=\frac{1}{\sqrt{2\pi \triangle x}}{exp \left(-\frac{x^2}{2{\triangle x}^2}\right)\ }dx\left(1\right),\]где $\triangle x$- малое изменение координаты частицы, вследствие флуктуации.
Рассмотрим положение Броуновской частицы через некоторые фиксированные промежутки времени. Начало координат поместим в точку, в которой частица находилась при t=0. Обозначим $\overrightarrow{q_i}$ -- вектор, который характеризует перемещение частицы между (i-1) и i наблюдениями. По истечении n наблюдений частица сместится из нулевого положения в точку с радиус-вектором $\overrightarrow{r_n}$. При этом:
\[\overrightarrow{r_n}=\sum\limits^n_{i=1}{\overrightarrow{q_i}}\left(2\right).\]Перемещения частицы происходит по сложной ломаной линии все время наблюдений.
Найдем средний квадрат удаления частицы от начала после n шагов в большой серии опытов:
\[\left\langle r^2_n\right\rangle =\left\langle \sum\limits^n_{i,j=1}{q_iq_j}\right\rangle =\sum\limits^n_{i=1}{\left\langle {q_i}^2\right\rangle }+\sum\limits^n_{i\ne j}{\left\langle q_iq_j\right\rangle }\left(3\right)\]где $\left\langle q^2_i\right\rangle $- средний квадрат смещения частицы на i- м шаге в серии опытов (он для всех шагов одинаков и равен какой-то положительной величине a2), $\left\langle q_iq_j\right\rangle $- является средней величиной скалярного произведения при i-м шаге на перемещение при j-м шаге в различных опытах. Эти величины независимы друг от друга, одинаково часто встречаются как положительные значения скалярного произведения, так и отрицательные. Поэтому, считаем, что $\left\langle q_iq_j\right\rangle $=0 при$\ i\ne j$. Тогда имеем из (3):
\[\left\langle r^2_n\right\rangle =a^2n=\frac{a^2}{\triangle t}t=\alpha t=\left\langle r^2\right\rangle \left(4\right),\]где $\triangle t$- промежуток времени между наблюдениями; t=$\triangle tn$ - время, в течение которого средний квадрат удаления частицы стал равен $\left\langle r^2\right\rangle .$ Получаем, что частица удаляется от начала. Существенно то, что средний квадрат удаления растет пропорционально первой степени времени. $\alpha \ $- можно найти экспериментально, а можно теоретически, как будет показано в примере 1.
Броуновская частица движется не только поступательно, но и вращаясь. Среднее значение угла поворота $\triangle \varphi $ броуновской частицы за время t равно:
\[{\triangle \varphi }^2=2D_{vr}t(5),\]где $D_{vr}$ -- коэффициент вращательной диффузии. Для сферической броуновской частицы радиуса - а $D_{vr}\ $ равен:
\[D_{vr}=\frac{kT}{8\pi \eta a^3}\ \left(6\right),\]где $\eta $ - коэффициент вязкости среды.
Броуновское движение ограничивает точность измерительных приборов. Предел точности зеркального гальванометра определяется дрожание зеркальца, подобно броуновской частице, которая подвергается ударам молекул воздуха. Случайное движение электронов вызывает шумы в электрических сетях.
Задание: Для того, чтобы математически полно охарактеризовать броуновское движение, надо найти $\alpha $ в формуле $\left\langle r^2_n\right\rangle =\alpha t$. Считать коэффициент вязкости жидкости известным и равным b, температура жидкости T.
Решение:
Запишем уравнение движения броуновской частицы в проекции на ось Ox:
\[m\ddot{x}=-b\dot{x}+F_x\ \left(1.1\right),\]где m -- масса частицы, $F_x$ -- случайная сила, действующая на частицу, $b\dot{x}$- член уравнения, характеризующий силу трения, действующая на частицу в жидкости.
Аналогичный вид имеют уравнения для величин, относящиеся к другим координатным осям.
Умножим обе части уравнения (1.1) на x, а члены $\ddot{x}x\ и\ \dot{x}x$ преобразуем:
\[\ddot{x}x=\ddot{\left(\frac{x^2}{2}\right)}-(\dot{x})^2,\dot{x}x=(\frac{x^2}{2}\ )(1.2)\]Тогда уравнение (1.1) приведем к виду:
\[\frac{m}{2}(\ddot{x^2})-m(\dot{x})^2=-\frac{b}{2}\left(\dot{x^2}\right)+F_xx\ (1.3)\]Усредним обе части этого уравнения по ансамблю броуновских частиц, учитывая при этом, что средняя от производной по времени равна производной от средней величины, так как это усреднение по ансамблю частиц, и, значит, переставим операцией дифференцирования по времени. В результате усреднения (1.3) получаем:
\[\frac{m}{2}\left(\left\langle \ddot{x^2}\right\rangle \right)-\left\langle m(\dot{x})^2\right\rangle =-\frac{b}{2}\left(\dot{\left\langle x^2\right\rangle }\right)+\left\langle F_xx\right\rangle \ \left(1.4\right).\]Так как отклонения броуновской частицы в любом направлении равновероятны, то:
\[\left\langle x^2\right\rangle =\left\langle y^2\right\rangle =\left\langle z^2\right\rangle =\frac{\left\langle r^2\right\rangle }{3}\left(1.5\right)\]Используем $\left\langle r^2_n\right\rangle =a^2n=\frac{a^2}{\triangle t}t=\alpha t=\left\langle r^2\right\rangle $, получаем $\left\langle x^2\right\rangle =\frac{\alpha t}{3}$, следовательно: $\dot{\left\langle x^2\right\rangle }=\frac{\alpha }{3}$, $\left\langle \ddot{x^2}\right\rangle =0$
Из-за случайного характера силы $F_x$ и координаты частицы x и их независимости друг от друга должно выполняться равенство $\left\langle F_xx\right\rangle =0$, тогда (1.5) сводится к равенству:
\[\left\langle m{\dot{\left(x\right)}}^2\right\rangle =\frac{\alpha b}{6}\left(1.6\right).\]По теореме о равномерном распределении энергии по степеням свободы:
\[\left\langle m{\dot{\left(x\right)}}^2\right\rangle =kT\left(1.7\right).\] \[\frac{\alpha b}{6}=kT\to \alpha =\frac{6kT}{b}.\]Таким образом, получим формулу для решения задачи о Броуновском движении:
\[\left\langle r^2\right\rangle =\frac{6kT}{b}t\]Ответ: Формула $\left\langle r^2\right\rangle =\frac{6kT}{b}t$ решает задачу о броуновском движении взвешенных частиц.
Задание: Частицы гуммигута сферической формы радиуса r участвуют в броуновском движении в газе. Плотность гуммигута $\rho $. Найти среднеквадратичную скорость частиц гуммигута при температуре T.
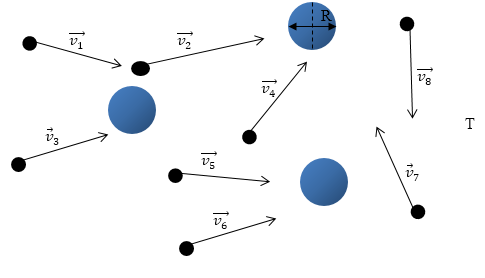
Рис. 1
Решение:
Среднеквадратичная скорость молекул равна:
\[\left\langle v^2\right\rangle =\sqrt{\frac{3kT}{m_0}}\left(2.1\right)\]Броуновская частица находится в равновесии с веществом, в котором она находится, и мы можем рассчитать ее среднеквадратичную скорость, используя формулу для скорости молекул газа, которые, в свою очередь, двигаясь, заставляют перемещаться броуновскую частицу. Для начала найдем массу частицы:
\[m_0=\rho V=\frac{4}{3}\pi R^3\rho \left(2.2\right)\]Тогда
\[\left\langle v^2\right\rangle =\sqrt{\frac{9kT}{4\pi R^3\rho }}\]Ответ: Скорость частицы гуммигута взвешенного в газе можно найти как $\left\langle v^2\right\rangle =\sqrt{\frac{9kT}{4\pi R^3\rho }}$.














