Существует три признака равенства для двух треугольников. В этой статье мы рассмотрим их в виде теорем, а также приведем их доказательства. Для этого вспомним, что фигуры будут равны в том случае, когда они будут целиком накладываться друг на друга.
Первый признак
Два треугольника будут равными, если две стороны и угол между ними одного из треугольников будут равняться двум сторонам и углу, лежащему между ними в другом.
Доказательство.
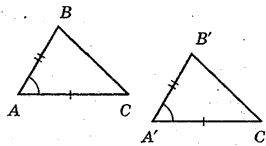
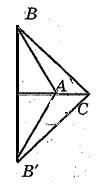
Рассмотрим два треугольника $ABC$ и $A'B'C'$, в которых $AB=A'B'$,$AC=A'C'$ и $∠A=∠A'$ (рис. 1).
Совместим высоты $A$ и $A'$ этих треугольников. Так как углы при этих вершинах равны между собой, то стороны $AB$ и $AC$ наложатся, соответственно, на лучи $A'B'$ и $A'C'$. Так как эти стороны попарно равны, то стороны $AB$ и $AC$, соответственно, совпадут со сторонами $A'B'$ и $A'C'$, а следовательно и вершины $B$ и $B'$, $C$ и $C'$ будут совпадать.
Следовательно, сторона BC полностью совпадет со стороной $B'C'$. Значит, и треугольники будут целиком накладываться друг на друга, что и означает их равенства.
Теорема доказана.
Второй признак
Два треугольника будут равными, если два угла и их общая сторона одного из треугольников будут равняться двум углам и их общей стороны в другом.
Доказательство.
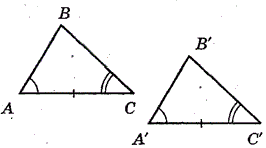
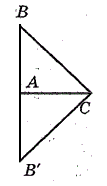
Рассмотрим два треугольника $ABC$ и $A'B'C'$, в которых $AC=A'C'$ и $∠A=∠A'$, $∠C=∠C'$ (рис. 2).
Совместим стороны $AC$ и $A'C'$ этих треугольников, так что высоты $B$ и $B'$ будут лежать по одну сторону от нее. Так как углы при этих сторонах попарно равны между собой, то стороны $AB$ и $BC$ наложатся, соответственно, на лучи $A'B'$ и $B'C'$. Следовательно, и точка $B$ и точка $B'$ будет точками пересечения совмещенных лучей (то есть, к примеру, лучей $AB$ и $BC$). Так как лучи могут иметь только одну точку пересечения, то точка $B$ совпадет с точкой $B'$. Значит, и треугольники будут целиком накладываться друг на друга, что и означает их равенства.
Теорема доказана.
Третий признак
Два треугольника будут равными, если три стороны одного из треугольников будут равняться трем сторонам в другом.
Доказательство.
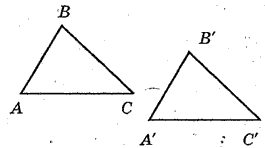
Рассмотрим два треугольника $ABC$ и $A'B'C'$, в которых $AC=A'C'$, $AB=A'B'$ и $BC=B'C'$ (рис. 3).
Доказательство.
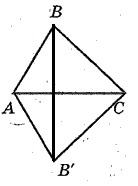
Совместим стороны $AC$ и $A'C'$ этих треугольников, так что высоты $B$ и $B'$ будут лежать по разную сторону от нее. Далее будем рассматривать три различных случая полученного после этого расположения этих вершин. Будем их рассматривать на рисунках.
Первый случай:
Так как $AB=A'B'$, то будет верно равенство $∠ABB'=∠AB'B$. Аналогично, $∠BB'C=∠B'BC$. Тогда, как сумму, получим $∠B=∠B'$
Следовательно, по теореме 1, эти треугольники равны.
Второй случай:
Так как $AB=A'B'$, то будет верно равенство $∠ABB'=∠AB'B$. Аналогично, $∠BB'C=∠B'BC$. Тогда, как разность, получим $∠B=∠B'$
Следовательно, по теореме 1, эти треугольники равны.
Третий случай:
Так как $BC=B'C'$, то будет верно равенство $∠ABC=∠AB'C$
Следовательно, по теореме 1, эти треугольники равны.
Теорема доказана.
Пример задач
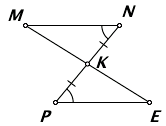
Докажите равенство треугольников на рисунке ниже
Доказательство.
Углы $MKN$ и $PKE$ будут вертикальными. Следовательно, $∠MKN=∠PKE$. Значит, с учетом условия задачи, треугольники будут равны по теореме 2.
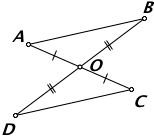
Докажите равенство треугольников на рисунке ниже
Доказательство.
Углы $AOB$ и $DOC$ будут вертикальными. Следовательно, $∠AOB=∠DOC$. Значит, с учетом условия задачи, треугольники будут равны по теореме 1.
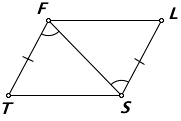
Докажите равенство треугольников на рисунке ниже
Доказательство.
Так как сторона $FS$ является общей для этих треугольников, то, с учетом условия задачи, треугольники будут равны по теореме 1.