Начальные сведения о треугольниках
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Точки в рамках определения 1 называются вершинами треугольника.
Отрезки в рамках определения 1 называются сторонами треугольника.
Треугольник будем обозначать тремя точками его вершин (рис. 1)
Медиана
Введем такое понятие, связанное с треугольниками как медиана.
Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.
Для более легкого запоминания можно пользоваться следующей «шуточной» иллюстрацией (рис. 2):
Очевидно, что треугольник имеет три медианы. Для них справедлива следующая теорема (её доказательство в этой статье рассматривать не будем):
Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.
Биссектриса
Введем такое понятие, связанное с треугольниками как биссектриса.
Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.
Для более легкого запоминания можно пользоваться следующей «шуточной» иллюстрацией (рис. 3):
Очевидно, что треугольник имеет три биссектрисы. Для них справедлива следующая теорема (её доказательство в этой статье рассматривать не будем):
Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.
Высота
Введем такое понятие, связанное с треугольниками как высота.
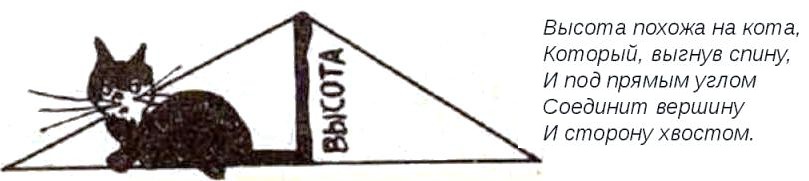
Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.
Для более легкого запоминания можно пользоваться следующей «шуточной» иллюстрацией (рис. 4):
Очевидно, что треугольник имеет три высоты. Для них справедлива следующая теорема (её доказательство в этой статье рассматривать не будем):
Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.
Пример задач
Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то $AB=BC$.
Доказательство
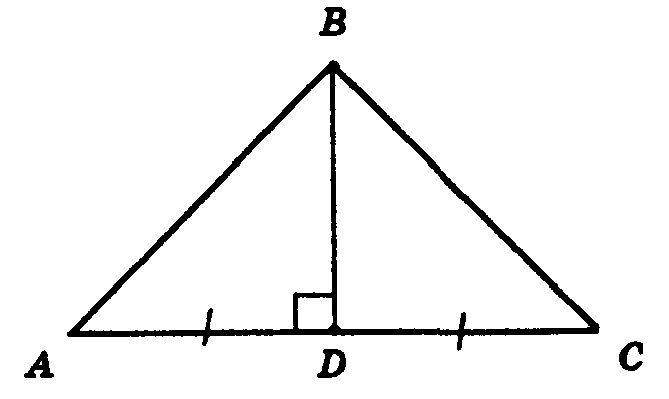
Изобразим рисунок по условию задачи (рис. 5).
Так как $BD$ является медианой, то по определению 4 будет верно равенство $AD=DC$
Так как $BD$ является высотой, то по определению 6 будет верно равенство $∠ADB=∠BDC=90^0$
У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.
Пусть нам даны равные треугольники $ABC$ и $A'B'C'$. В них проведены высоты $BH$ и $B'H'$, соответственно. Доказать, что эти высоты в треугольниках будут равны между собой.
Доказательство.
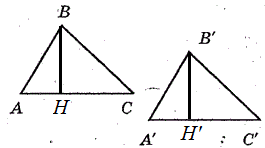
Изобразим рисунок по условию задачи (рис. 6).
Так как данные треугольники равны, то будет верно равенство $∠A=∠A'$
Так как $BH$ и $B'H'$ являются высотами, то по определению 6 будет верно равенство $∠AHB=∠A'H'B'=90^0$
Из треугольника $ABC$, имеем
$∠ABH=180^0-90^0-∠A=90^0-∠A$
Из треугольника $A'B'C'$ и равенства углов $∠A$ и $∠A'$, получим
$∠A'B'H'=180^0-90^0-∠A'=90^0-∠A'=90^0-∠A=∠ABH$
По всему сказанному выше, треугольники $AHB$ и $A'B'H'$ равняются по первому признаку. Но тогда и стороны $BH$ и $B'H'$ равны.