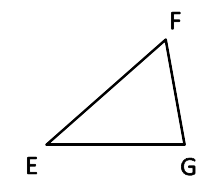Понятие треугольника
Вспомним следующую аксиому для такого основного понятия геометрии, как прямая.
Аксиома 1: Можно найти как минимум три точки, которые не будут лежать на одной и той же прямой.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда:
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Точки в рамках определения 1 называются вершинами треугольника.
Отрезки в рамках определения 1 называются сторонами треугольника.
Треугольник будем обозначать тремя точками его вершин (рис. 1).
Рисунок 1. Треугольник EFG. Автор24 — интернет-биржа студенческих работ
Виды треугольников
Треугольники можно разделять на различные виды по углам и по сторонам треугольника. Рассмотрим для начала, какие бывают виды треугольников в различии от их углов.
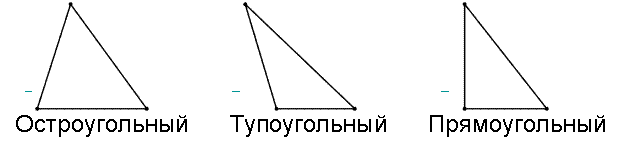
Треугольник будем называть остроугольным, если все углы в нем менее 900.
Треугольник будем называть тупоугольным, если один из углов в нем более 900.
Треугольник будем называть прямоугольным, если один из углов в нем равен 900.
Все эти виды изображены на рисунке 2.
Рисунок 2. Виды треугольников. Автор24 — интернет-биржа студенческих работ
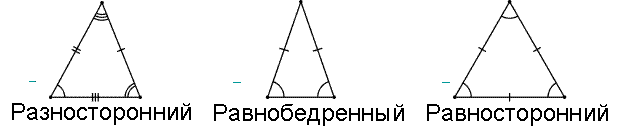
По сторонам треугольники разделяются на разносторонние, равнобедренные и равносторонние.
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Треугольник будем называть равносторонним, если три его стороны будут равны между собой.
Все эти виды треугольников изображены на рисунке 3.
Рисунок 3. Виды треугольников. Автор24 — интернет-биржа студенческих работ
Свойства треугольников
Введем теперь некоторые свойства треугольников в виде теорем. В данной статье доказательства их мы рассматривать не будем.
Вначале приведем теоремы, которые относятся ко всем видам треугольников. Но для них нам будут необходимы еще несколько понятий.
Медианой будем называть отрезок, который соединяет вершину с серединой противоположной стороны.
Биссектрисой будем называть луч, который проведен из вершины так, что делит угол в этой вершине на две равные части.
Высотой будем называть отрезок, который проведен из вершины так, что падает на противоположную сторону под прямым углом.
Все три медианы в треугольнике пересекаются в единственной точке, которая будет называться центроидом треугольника.
Все три биссектрисы в треугольнике пересекаются в единственной точке, которая будет называться инцентром треугольника.
Все три высоты в треугольнике пересекаются в единственной точке, которая будет называться ортоцентром треугольника.
Следующие две теоремы рассматривают свойства для равнобедренных треугольников.
Углы при основании равнобедренного треугольника будут равными.
Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.
Отметим, что теоремы, относящиеся к равнобедренным треугольникам также справедливы и для равносторонних треугольников.
Пример задачи
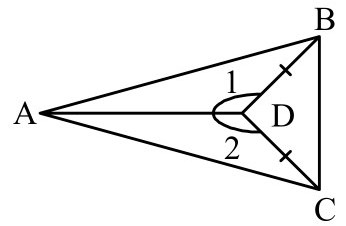
Пусть дан треугольник ABC. Доказать, что он будет равнобедренным в условиях рисунка 5.
Рисунок 4. Треугольник. Автор24 — интернет-биржа студенческих работ
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона BD равняется стороне CD. Так как у треугольников ADB и ADC сторона AD является общей, то треугольники ADB и ADC будут равняться по первому признаку. Но тогда и стороны AB и AC также равны между собой. Следовательно, данный треугольник будет равнобедренным.